PCA Color Augmentationを拡張してTensorFlow/Keras向けに実装した

---

PCA Color AugmentationはAlexNetの論文に示された画像向けのData Augmentationですが、画像用だけではなく、テンソルの固有値分解をすることで構造化データに対しても使えるようにしてみました。これの解説と効果を書きます。

リポジトリ

こちら　https://github.com/koshian2/PCAColorAugmentation

PCA Color Augmentationとは？

AlexNetの論文に出てきた画像向けData Augmentationアルゴリズム。主成分分析を用いて、カラーチャンネルあたりの固有値、固有ベクトルを計算し、それをもとに色（データ）の分布に見合ったノイズを付加する。

一言で言えば、よく用いられているカラーチャンネルシフトよりもかなり自然で賢いアルゴリズムですね。AlexNet自体はディープラーニングの論文で1､2を争うぐらい引用されているのに、このアルゴリズムはあまり注目されないのが不思議です。実際にCIFAR-10で動かしてみると以下のようになります。

かなり自然な調整になっています。まるで自然光の加減をいじっているようですね。

構造化データへの応用

これの本質とは、構造化データへの応用可能であるということではないかと自分は思います。画像でのPCA Color Augmentationはカラーチャンネル間の固有値、固有ベクトルを求めることですが、カラーチャンネルを系列に読み替えると構造化データでも使えるということになります。

Irisデータセットでやってみました。

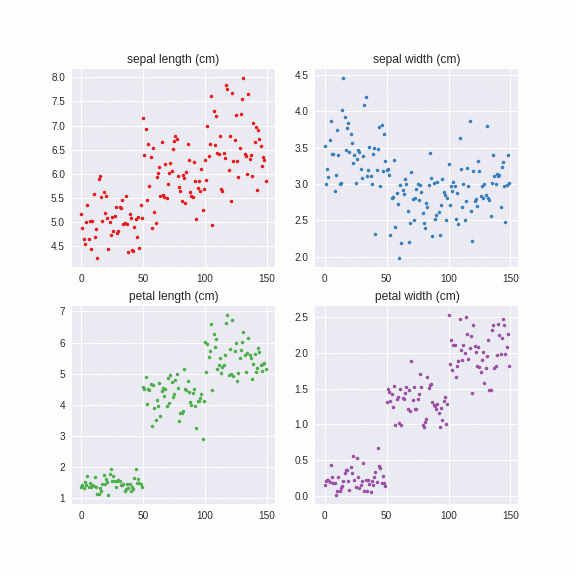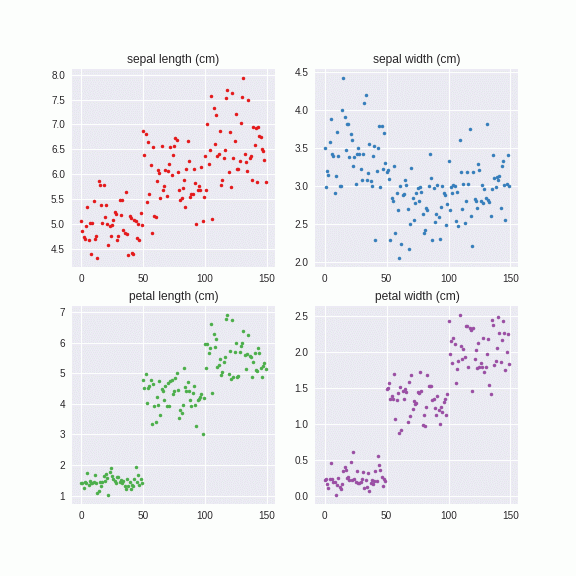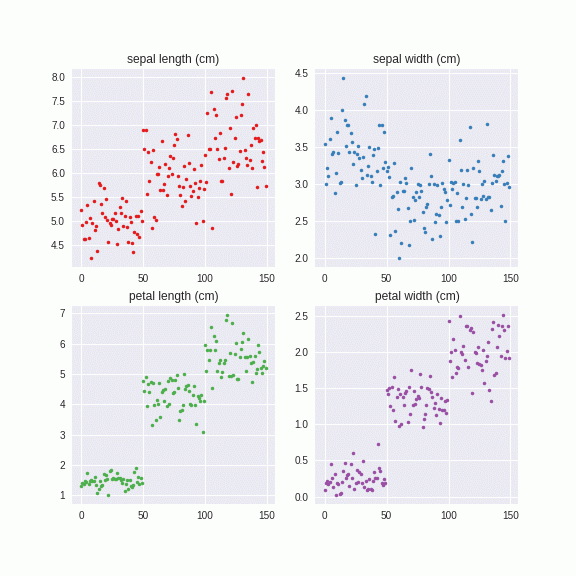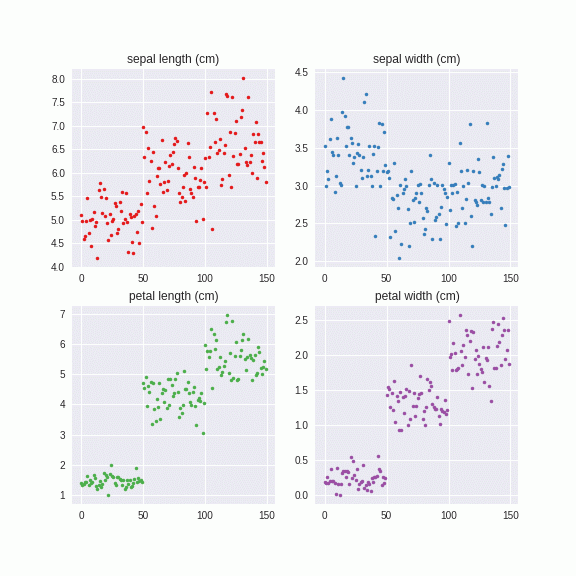
このように系列別に自然なノイズを付与することができました。これは乱数から出しているので、無限に生成することができます。つまり、データがあたかも大量にあるような効果が得られ、正則化効果をもたらすものと予想されます。

ちなみにさっきのIrisは一括でやった例ですが、やっていることはテンソルの固有値分解なので、データを系列ごとのテンソルに変えてPCA Augmentationをすると、カテゴリー別のAugmentationができます。

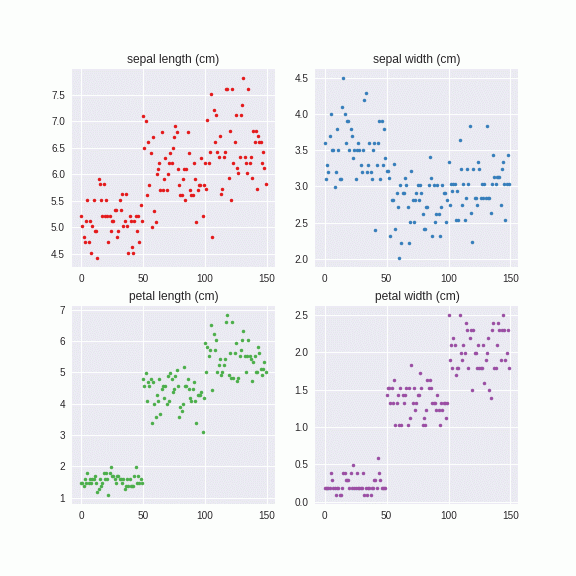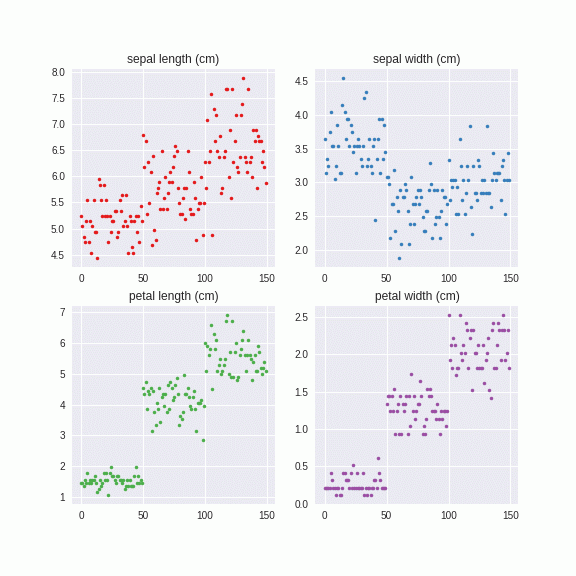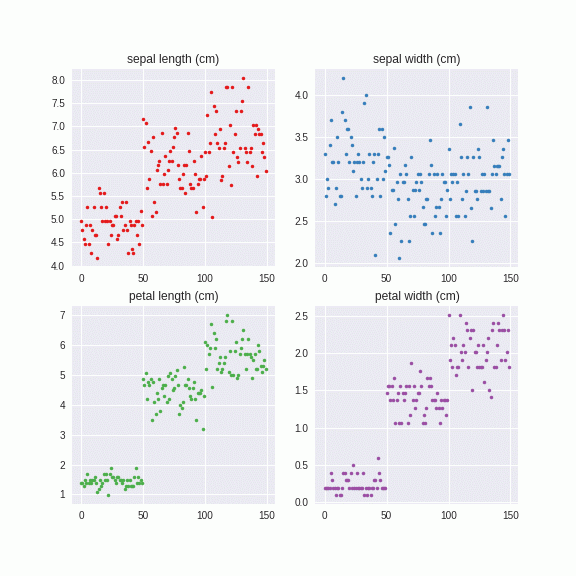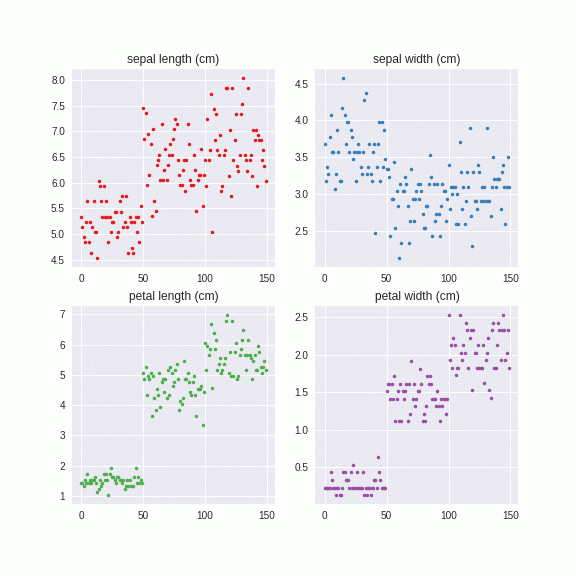
このように、カテゴリーごとにに異なる固有値、固有ベクトルを計算し、それを系列にノイズを与えています。つまり、カテゴリーA,カテゴリーBとあたかも異なるデータセットのように解釈しています。こちらのほうがより直感的ではないでしょうか。

アルゴリズム解説

やっていることは主成分分析ですが、入力のテンソルの次元について解説します。

データの入力次元

2階テンソル～5階テンソルまで考えます。階数別に具体的にどういう形式で入っているか場合分けします。

• 2階 $(batch, ndim)$　例：Irisなどの構造化データ
• 3階 $(batch, step, ndim)$　例：時系列データ
• 4階 $(batch, H, W, ch)$　例：画像
• 5階 $(batch, D, H, W, ch)$　例：動画

4階以上の場合はHとWの次元を結合します。$ndim=H\times W$とします。

• 4階 $(batch, ndim, ch)$
• 5階 $(batch, D, ndim, ch)$

分散共分散行列

主成分分析は分散共分散行列の固有値問題なので、テンソルの下2階についての分散共分散行列を計算します。分散共分散行列は以下のような次元になります。

• 2階 $(ndim, ndim)$
• 3階 $(batch, ndim, ndim)$
• 4階 $(batch, ch, ch)$
• 5階 $(batch, D, ch, ch)$

固有値・固有ベクトル

固有値の次元は次のようになります。

• 2階 $(ndim, )$
• 3階 $(batch, ndim)$
• 4階 $(batch, ch)$
• 5階 $(batch, D, ch)$

固有ベクトルの次元は分散共分散行列と等しくなります。

乱数

次に平均0、標準偏差0.1（デフォルト、変更可能）の正規乱数を発生させます。2階のときのみ特殊で入力と同じ次元、3階以上のときは固有値と同じ次元の乱数を発生させます。

• 2階 $(batch, ndim)$
• 3階 $(batch, ndim)$
• 4階 $(batch, ch)$
• 5階 $(batch, D, ch)$

2階の場合の増分

2階の場合の増分は少し特殊で、固有値に新しい軸を作り$(1, ndim)$とします。それと乱数をかけ、$(batch, ndim)$の変数ができます。これに固有ベクトルを右側からかけ、matmulで計算すると$(batch, ndim)$の増分変数が出来上がります。2階の場合はひとまずここで終わりです。

3階以上の場合の増分

乱数は固有値と同じ次元で発生させました。まずはこの乱数×固有値を計算し、これの末尾に新しい軸を作ります。そして、固有ベクトルをmatmulで左側からかけます。一連の流れは次のようになります。

• 3階 $(batch, ndim, ndim)(batch, ndim, 1)=(batch, ndim, 1)$
• 4階 $(batch, ch, ch)(batch, ch, 1)=(batch, ch, 1)$
• 5階 $(batch, D, ch)(batch, D, ch, 1)=(batch, ch, 1)$

末尾の1の次元を削除します。

• 3階 $(batch, ndim)$
• 4階 $(batch, ch)$
• 5階 $(batch, D, ch)$

3階と4階の場合は2つ目、5階の場合は3つ目に新しい軸を作ります。これは消えてしまった軸の復元です。

• 3階 $(batch, 1[step], ndim)$
• 4階 $(batch, 1[ndim], ch)$
• 5階 $(batch, D, 1[ndim], ch)$

3階の場合はここで終わりです。4階と5階の場合のみ続きます。最初にHとWを結合させた変数と同じ次元にブロードキャストさせます。

• 4階 $(batch, ndim, ch)$
• 5階 $(batch, D, ndim, ch)$

最後の、4階と5階を入力次元と同じになるようにReshapeします。これで終わりです。

• 4階 $(batch, H, W, ch)$
• 5階 $(batch, D, H, W, ch)$

これで全部の階数の増分を計算をすることができました。全てのケースで増分はブロードキャストをかませると入力次元と等しくなります。

スケール調整

次に、入力変数に応じた増分のスケーリングを行います。これは例えば画像なら0～255のスケールで計算するか、0～1のスケールで計算するかのためのもので、基本的には1のままでいいです。後のクリッピングにも関係します。0～255のスケールで計算する場合のみ、scale=255で入力してください。

クリッピング

スケール調整した増分を入力テンソルに足します。

デフォルトではONになっています。ONの場合のみ、画像では0～1のスケールなら範囲を0～1にするように頭打ち、前のスケールで1以外の値を入力していたら0～スケールになるようにします。基本的には画像向けなので、構造化データでやるときは切ったほうがいいと思います。

効果検証

CIFAR-10

VGGライクな簡単なモデルを作りました。

• 入力(32, 32, 3)
• 3×3畳み込み、32フィルター、same padding
• カーネル2のAveragePooling(16, 16, 32)
• 3×3畳み込み、64フィルター、same padding
• カーネル2のAveragePooling(8, 8, 64)
• 3×3畳み込み。128フィルター、same padding
• 全結合化(8192, )
• 10のSoftmax

PCA Color Augmentationを入れるかどうか、畳み込みにBatch Normalizationを入れるかどうかの計4条件で比較しています。これはAlexNetの登場がBatchNormalizationの登場前だったからです。PCA Color Augmentation以外のData Augmentationや、その他の正則化は切っています。

PCA　Augmenation	Batch Norm	訓練精度	検証精度	秒/エポック(GPU)	秒/エポック(CPU)
○	○	0.9931	0.7618	94	14
○	☓	0.9208	0.6651	92	14
☓	○	1.0000	0.7762	6	–
☓	☓	0.9843	0.6507	6	–

※CPU,GPUはPCA Color Augmentationを動かしているデバイスです。訓練自体はどちらもGPUで行っています。Colab のGPUを使っています。

精度だけ見ると、BatchNormを入れないのなら、PCA Color Augmentationは1.5%ほど精度の上昇に寄与しているというのが言えます。

PCA Augmentationを入れてBatchNormを入れなかったケースより、PCA Augmentationを入れなくてBatchNormを入れたケースを比較すると、精度が11%ぐらい高くなっていますが、これはBatchNormが強すぎるのと、CIFAR-10のデータの性質による部分も大きいのと思います。
CIFAR-10はある学習率（あるいは学習のステップ）をだんだん落としていくと異様に精度が上がるという特徴があります。これはリアルのデータセットではあまり見ないようなケースで、CIFAR-10特有の現象ではないでしょうか。つまり、学習率調整ゲーになってしまうから、訓練精度が100%近くなって異様にステップが小さくなると学習率をへらすのとほぼ同じ効果があるということだと思います。

「BatchNormを入れたらPCA不要っすよね？」と言われたらそれはそうなんですが、BatchNorm使っててオーバーフィッティングに困ったケースで、最後にPCAを入れたら綺麗にオーバーフィッティングが解消されたようなケースもありました。PCA Color Augmentationは画像への作用だけで完結するので、物体検出やランドマーク検出でもアノテーションの変換をせずに使いやすいのですよね。なので、「そういうのもあるんだな」ぐらいで頭の片隅に入れておいてもいいのではないでしょうか。

計算量についても補足しておきましょう。PCA Color Augmentationのデメリットは計算の重さです。しかも固有値の計算に用いている特異値分解（SVD）がTensorFlowのGPUで動かすとCPUより明らかに遅いという現象があります。

上記の計測結果ではGPUでAugmentationした場合は、CPUでAugmentatoinした場合より7倍近く遅くなってしまいました。あまりに遅かったので、同様のコードをNumpyベースに移植したところ、かなりマシになりました（94秒が14秒に縮んだ）。最新のデバイスだとマシになっているのかもしれませんが、Numpyのテンソルバージョンを使うことをおすすめします。

ちなみにこの現象は前から報告されていて、既にIssueが立っています。CUDAの改良待ちというところでしょうか。

SVD on GPU is slower than SVD on CPU
https://github.com/tensorflow/tensorflow/issues/13603

PyTorchのSVDはそこそこ速いそうですが、PyTorchのSVDではテンソル分解ができない（行列限定になってしまう）のでなかなか困ったものです。結局そこはCPUになっちゃうのかな。

Wineデータセット

次は構造化データの例です。SklearnのWineデータセットを使いました。ただ、このまま訓練させると検証精度も100%近くなってなかなかオーバーフィッティングしてくれないので、擬似的にオーバーフィッティングを再現してみました。以下のようにしました。

• 通常は訓練：テスト＝7：3で分割するところを、3：7で分割し、訓練データが少ない状況を再現する（オーバーフィッティングしやすくなる）
• 入力次元が13のところを、隠れ層を「→256→128→64→32→3」と過剰に導入し、オーバーフィッティングしやすくする

PCA Augmentationなし、ありでシンプルに全体をAugmentationさせる）、ありでカテゴリー別にAugmentationさせるケースで比較しました。

PCA Augmentation	PCA回数	検証精度
なし	0	0.9440
あり（全体一括）	5	0.9600
あり（全体一括）	20	0.9760
あり（カテゴリー別）	5	0.9600
あり（カテゴリー別）	20	0.9680

こちらはかなり効果があったように見えます。PCA回数は何回PCA Augmentationさせるかで、回数が多いほどAugmentationにより擬似的に生成されたデータが増えます。例えばデータ数が100で1回Augmentationさせたら100個できますし、20回させたら2000個擬似データができます。

まとめ

PCA Color Augmentationを実装して、効果を確認することができました。画像ではBatchNormが強すぎてこの効果が潰れてしまうことがありましたが、何らかの機会で正則化が必要になったら使ってみると面白いと思います。

PCA Color Augmentationを構造化データにも適用しましたが、構造化データのほうが効果がわかりやすく出たのが興味深かったです。

---

---

Shikoan's ML Blogの中の人が運営しているサークル「じゅ～しぃ～すくりぷと」の本のご案内

---