論文まとめ:Rewrite the Stars

ニューラルネットワークにおける要素ごとの積が多項式カーネルと同様に入力を高次元の非線形空間へ写像する理論的根拠を示し、スター演算を活用した効率的な「StarNet」を提案している。ImageNetを用いた実験で表現力と推論速度を両立する有効性が示され、既存の軽量モデルを上回る性能を達成した。
- タイトル:Rewrite the Stars
- 著者:Xu Ma, Xiyang Dai, Yue Bai, Yizhou Wang, Yun Fu
- 論文URL:https://arxiv.org/abs/2403.19967
- カンファ:CVPR 2024
- GitHub:https://github.com/ma-xu/Rewrite-the-Stars
目次
論文要約 By Gemini 2.5
・この論文において解決したい課題は何?
要素ごとの積(スター演算)がなぜニューラルネットワークで高い性能を示すのか、その根本的な理由を解明し、特に効率的なネットワーク設計にどう活かせるかという課題に取り組んでいます。
・先行研究だとどういう点が課題だった?
スター演算の有効性について、直感的な説明(変調メカニズム、高次特徴など)は存在しましたが、その効果を裏付ける包括的な理論的分析や強力な証拠が不足していました。
・先行研究と比較したとき、提案手法の独自性や貢献は何?
スター演算が、入力特徴量を暗黙的に非常に高次元な非線形特徴空間へ写像する能力を持つことを理論的に解明し、これが多項式カーネル関数と類似していることを示しました。また、この知見に基づき、効率的なネットワークモデル「StarNet」を提案し、その有効性を示した点が貢献です。
・提案手法の手法を初心者でもわかるように詳細に説明して
提案手法の中心は「スター演算」です。これは、2つの特徴量ベクトルやテンソルを、対応する要素同士で掛け算する単純な操作です。この操作により、元の特徴量の次元数dに対して、計算コストを増やさずに約(d^2)/2という非常に多くの新しい特徴(暗黙的な高次元特徴)が生まれます。これをネットワーク内で複数回繰り返すと、さらに爆発的に特徴の次元が増え、表現力が向上します。このスター演算を活用して、シンプルで効率的な「StarNet」という画像認識モデルを構築しました。
・提案手法の有効性をどのように定量・定性評価した?
定量的評価として、スター演算と単純な和算を比較する「DemoNet」での画像分類精度(ImageNet-1k)、ネットワークの幅や深さを変えた際の影響を検証しました。また、提案モデル「StarNet」を他の軽量モデルと比較し、精度と推論速度(CPU, GPU, iPhone)で優位性を示しました。
定性的評価として、2次元のトイデータセット上で、スター演算と和算、さらにSVMのカーネル関数(多項式、ガウス)との決定境界を可視化し比較しました。
・この論文における限界は?
提案モデルStarNetは概念実証であり、性能を極限まで高めるためのハイパーパラメータ調整や高度な設計技法は意図的に採用していません。また、スター演算によって生成される暗黙的な高次元空間の係数分布を最適化する方法はまだ限定的である点が挙げられます。
・次に読むべき論文は?
スター演算の理論的背景や応用に関心があれば、以下のような論文が参考になるでしょう。
* FocalNet [60], HorNet [45], VAN [18]: 本論文でも言及されている、スター演算を活用したコンピュータビジョン分野の先行研究。
* Mamba [17], Hyena Hierarchy [44]: 自然言語処理分野でスター演算に類似したアプローチを用いている研究。
* PolyNL [2]: 自己注意機構と行列積の関係性を多項式展開の観点から分析しており、本論文の議論と関連性があります。
・論文中にコードが提示されていれば、それをリンク付きで示してください
はい、論文のAbstractの最後に以下のリンクが記載されています。
https://github.com/ma-xu/Rewrite-the-Stars
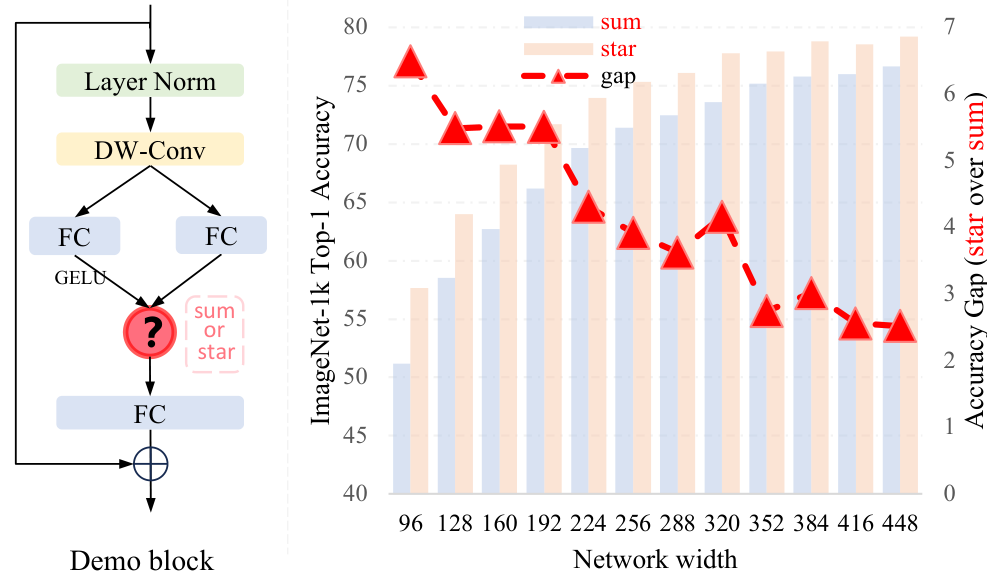
補足
- なぜ今更スター演算なのか?
- Attentionがトークン数の増加に対して二次関数的に増える
- スター演算(ドット積)の採用例は過去に非常に多い
- 本論文で主張したいポイント:Star演算の強力な代表能力を、Star演算が入力を極めて高次元の非線形特徴空間に写像する能力を持つ
- 異なるチャンネル間の特徴のペアワイズ乗算を行うカーネル関数、特に多項式カーネル関数
- コンパクトな特徴空間内でほぼ無限の次元を達成することを可能
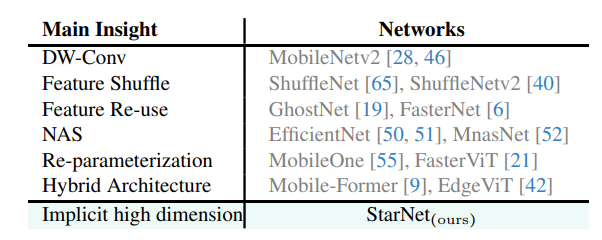
手法
- カーネル法とニューラルネットワークは異なる観点から非線形性を導入している
- 従来の機械学習→カーネル法
- ニューラルネットワーク→活性化関数
- カーネルトリックの原理と同様に、星型演算が低次元入力内で高次元かつ非線形な特徴空間を得ることができることを実証したい
理論


幅128の10層の等方性ネットワークが与えられたとき、暗黙の次元数は90の1024乗。これは無限次元として合理的に近似可能
Toy Example
- 簡易的な実験のための図1(最初の図)の簡単なネットワークを作ってみる。入力解像度を1/16にする畳み込み層と、特徴抽出のためのデモブロックの素朴な設計
- このような例はSVMのカーネルが得意で、プリミティブなニューラルネットワーク「Starなし(Sum Operation)」だと決定境界がうまく引けていない
- ニューラルネットワークでも「Star Operation」を入れることで決定境界が分離可能

オープンディスカッション
- 活性化関数は本当に不可欠なのか?
- 予備実験では、ニューラルネットワークの活性化関数を排除することの実現可能性は示せた
- スター演算は自己注意と行列の乗算とどのように関係するのか?
- 自己注意の行列乗算は要素ごとの乗算を共有することを実証可能
- 要素ごとの乗算(スター演算)とは対象的に、グローバルな相互作用を容易にできるが、入力形状が変わるために追加の演算(プーリング)が必要
- スター演算だとこの複雑さを回避できる
- 自己注意の有効性に関する新たなインサイトを提供し、先行研究の動的特徴の再検討に貢献する可能性がある
- 暗黙の高次元の係数分布をどのように最適化するか?
- 多項式カーネルはハイパーパラメータを通じて調整できるが、スター演算は分布を微調整できる範囲が限られる
- この制約は、極端に高い次元が中程度の性能向上しかもたらさない理由を説明するかもしれない
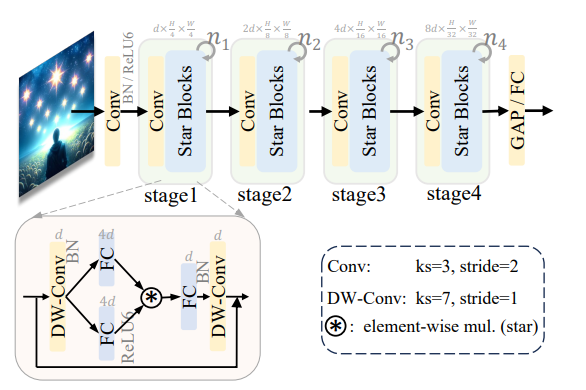
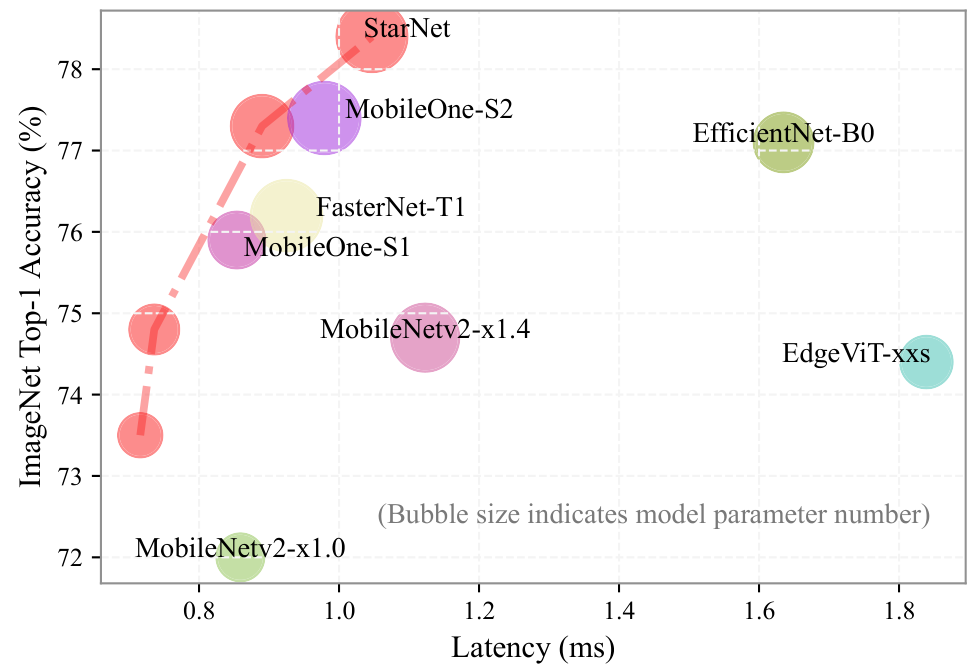
早いし高性能
ImageNetの性能
所感
タイトルかっこいいなって読んだらめっちゃしっかりした内容だった! LLM全盛期にこの手の論文出てくるのが珍しい
Shikoan's ML Blogの中の人が運営しているサークル「じゅ~しぃ~すくりぷと」の本のご案内
技術書コーナー
北海道の駅巡りコーナー

