RCNNで使われるSelective Searchについてまとめてみる

RCNNで用いられる「Selective Search」について中で何をやっているのかまとめてみました。RCNNの論文を読んでいるときによく出てくる「Selective Search」や「Region Proposal」といった用語が何を示しているのか、ソースコードを追うことで理解を進めます。
目次
Selective Searchって何?
オリジナルのRCNNで使われたRegion Proposalの抽出方法。一言で言えば「画像内の似ているピクセルをまとめるための教師なしアルゴリズム」という感じ。ただしめちゃくちゃアドホックなモデルで計算コストが重いので、FastRCNN、FasterRCNNと改良されるに連れ使われなくなってしまいました。
これを理解しても現状ありがたみはかなり薄いですが、Selective SearchとRegion Proposalのモヤっとした部分は解消するかもしれない。
RCNNの基本の発想
RCNNの発想は単純で、画像分類の延長線上にあります。画像分類が1枚の画像全体の分類をするのに対し、RCNNは1枚の画像を適当に切り取った領域を分類するというもの。切り取る領域をもっともらしくすれば物体検出に使えるという話です。
ただ、1枚の画像から切り取る組み合わせは無限にあるため、それっぽく切り取るためのアルゴリズムが必要です。RCNNでは、1枚の画像から切り取るための候補を大量に(2000枚以上)切り出して、切り出した画像に対して分類をかけています。この発想はFastRCNN、FasterRCNNと改良されていっても変わりません。
1枚の画像から、2000枚以上切り出した各”候補”のことをRegion Proposalといいます。Region Proposalは中間~後処理で統合されていくのですが(Non max supression)、候補(Proposal)を切り出すためのアルゴリズムとしてRCNNで用いているのがSelective Search。
まとめると、Region Proposalを切り出すためのアルゴリズムがSelective Search。
Selective Searchの大きな流れ
Selective Searchというのは今から見るとだいぶ古風なアルゴリズムで、ディープラーニングが普及する前なので、複雑かつアドホックな特徴量設計をしています。HOG特徴量をごにょごにょしてる頃のイメージで見ていけば雰囲気はわかるかもしれません。
Selective Searchは今実装してもほとんどありがたみがないので覚える必要はないですが、以下のリポジトリを元にしています。
https://github.com/AlpacaDB/selectivesearch
この中の「selectivesearch/selectivesearch.py」というファイルをベースに見ていきます。Selective Searchは以下の流れになります。
- Felzenszwalb法にて画像のセグメンテーション。セグメンテーションした各部分を1つのRegionとする。(skimageに組み込み関数あり)
- 各Regionの、色とテクスチャについてヒストグラムベースの特徴量を作る。
- 全てのRegionの組み合わせについて、Region同士が重なってる(Intersectしている)組み合わせを全列挙。これらをNeighborとする。
- 全てのNeighborについて、2の特徴量から、「色、テクスチャ、サイズ、オーバーラップしてる領域」の4項目について、Region同士の類似度を計算。
- 類似度を元にHierarchal Searchをして、類似度が高いものをマージする
この5つからなるのがSelective Searchです。結構面倒くさいことやっています(コードは読みやすいです)。
各段階をそれぞれ見ていきましょう。
1. Felzenszwalb法による画像のセグメンテーション
画像の似たような領域をセグメンテーション(Semantic Segmentationと似たイメージでOK)しましょうというのがここでの目的。ここで使っているのはFelzenszwalb and Huttenlocherによるにグラフベースのアルゴリズム。詳しい解説はこっち。グラフ理論とUnion Findを使っており、1から実装するととても面倒くさそう(素人並感)。
ここでは「使えればいい」でさっさと先に進みたいので、Skimageの組み込み関数を使ってみましょう。
import skimage
import skimage.segmentation
import matplotlib.pyplot as plt
def felzenszwalb():
img = skimage.data.astronaut()
scales = [100, 300, 100, 100]
sigmas = [0.5, 0.5, 0.8, 0.5]
min_sizes = [50, 50, 50, 200]
fig, ax = plt.subplots(2, 2, figsize=(10, 10), sharex=True, sharey=True)
for i, (sc, sg, ms) in enumerate(zip(scales, sigmas, min_sizes)):
segments = skimage.segmentation.felzenszwalb(img, scale=sc, sigma=sg, min_size=ms)
ax[i // 2][i % 2].imshow(skimage.segmentation.mark_boundaries(img, segments))
ax[i // 2][i % 2].set_title(f"scale={sc}, sigma={sg}, min_size={ms}")
plt.show()
if __name__ == "__main__":
felzenszwalb()
Skimageの公式ページを参考に、パラメーターを変えてセグメンテーションしてみました。Felzenszwalb法は「skimage.segmentation.felzenszwalb」でできます。
skimage.segmentation.felzenszwalbには「scale, sigma, min_size」という3つのパラメーターがあり、詳しくは割愛しますが分割領域のサイズを調整することができます。パラメーターを変えた結果は次のようになります。各パラメータを大きくすると大きい領域だけ残るようになります。

このように似たような領域同士を分割する手法の1つが、Felzenszwalb法なのです。これをベースにRegion ProposalのRegionを作っていきます。
2. ヒストグラムベースの特徴量を作る
最終的には重なり合うRegion同士のペアの類似度を計算したいのですが、類似度を計算するための指標としてヒストグラムベースの特徴量を作っていきます。
なぜヒストグラムベースなのかというと、Regionごとにサイズが違ってピクセル単位では比較できないからです。これはRCNNの論文にもSelective Searchの論文書いていなく、完全に自分の後付解釈なのですが、画像のヒストグラムの比較というのはWasserstein距離だからです(ヒストグラムの比較がEarth Mover Distanceそのもの)。GANの世界ではWGANで用いられている指標とイメージ的には似ています。Wikipediaソースですが、このように書かれています。
例えば計算機科学の分野においては、二つのデジタル画像の色ヒストグラム(英語版)といった離散分布を比較する際に、ワッサースタイン計量 W1 が広く用いられている。詳細についてはEMD(英語版)を参照されたい。
ヒストグラムベースの特徴量を作るコードは以下のようになります。GitHubのコードからです。
def _extract_regions(img):
R = {}
# get hsv image
hsv = skimage.color.rgb2hsv(img[:, :, :3])
# pass 1: count pixel positions
for y, i in enumerate(img):
for x, (r, g, b, l) in enumerate(i):
# initialize a new region
if l not in R:
R[l] = {
"min_x": 0xffff, "min_y": 0xffff,
"max_x": 0, "max_y": 0, "labels": [l]}
# bounding box
if R[l]["min_x"] > x:
R[l]["min_x"] = x
if R[l]["min_y"] > y:
R[l]["min_y"] = y
if R[l]["max_x"] < x:
R[l]["max_x"] = x
if R[l]["max_y"] < y:
R[l]["max_y"] = y
# pass 2: calculate texture gradient
tex_grad = _calc_texture_gradient(img)
# pass 3: calculate colour histogram of each region
for k, v in list(R.items()):
# colour histogram
masked_pixels = hsv[:, :, :][img[:, :, 3] == k]
R[k]["size"] = len(masked_pixels / 4)
R[k]["hist_c"] = _calc_colour_hist(masked_pixels)
# texture histogram
R[k]["hist_t"] = _calc_texture_hist(tex_grad[:, :][img[:, :, 3] == k])
return R
imgは(1)のFelzenszwalb法でセグメンテーションされた結果で4チャンネルからなります。RGBの他に区分けされた領域を示すラベルのインデックスが最後につきます。これを読むとヒストグラムベースの特徴量を作るのは、次のような流れであるのがわかります。
- 元の画像をRGB→HSV色空間変換したものをhsvとする
- 全てのRegionについて、Bounding Box方式に変換したものをRとする(上記コードのpass 1)
- RGB色空間ベースで、テクスチャの勾配を取る(上記コードのpass 2)
- Rの全ての領域に対し、マスクされたピクセル数(size)、HSV色空間ベースでのヒストグラム(hist_c)、テクスチャ勾配のヒストグラム(hist_t)を取る(上記コードのpass 3)
各passについて見ていきましょう。
1のHSV変換はそのままだし、2のBounding Box記法への変換はコード以上の説明をしようがないので省略します。
2-3. テクスチャの勾配を取る(pass 2)
pass 2の「_calc_texture_gradient」の部分を見てみましょう。
def _calc_texture_gradient(img):
"""
calculate texture gradient for entire image
The original SelectiveSearch algorithm proposed Gaussian derivative
for 8 orientations, but we use LBP instead.
output will be [height(*)][width(*)]
"""
ret = numpy.zeros((img.shape[0], img.shape[1], img.shape[2]))
for colour_channel in (0, 1, 2):
ret[:, :, colour_channel] = skimage.feature.local_binary_pattern(
img[:, :, colour_channel], 8, 1.0)
return ret
本来のSelective Searchではガウシアン微分フィルタ(ガウシアンぼかしを入れて差分を取るとか?)を使っていますが、この実装ではLBP(Local Binary Pattern)を取っています。LBPの詳しい説明はこちら。詳細は左の記事に譲りますが、LBPも微分フィルタもベースはエッジ検出のようなものです。LBPの場合は特にエッジの線の形状に対して普遍で、ヒストグラムを使ってテクスチャマッチングができます。この後ヒストグラムベースの特徴量を取るので、ここでLBPを使うのは自然といえるでしょう。
「普通の画像に対してLBPを取るとどうなるのか?」ということで試してみましょう。LBPを取る際は入力画像をグレースケール化(RGB→グレースケールの変換をするか、チャンネル単位でLBPを取るか)することに注意してください。
import skimage
import skimage.feature
import matplotlib.pyplot as plt
def lbp():
img = skimage.data.astronaut()
gray = skimage.color.rgb2gray(img)
lbp_val = skimage.feature.local_binary_pattern(gray, 8, 1.0)
fig, ax = plt.subplots(1, 2, figsize=(10, 5), sharex=True, sharey=True)
ax[0].imshow(gray, cmap="gray")
ax[1].imshow(lbp_val, cmap="gray")
plt.show()
if __name__ == "__main__":
lbp()

これだけだと何のために使うのかわかりづらいですが、「テクスチャの特徴量を取りたいんだな」ぐらいに思っておけばいいでしょう。
2-4. ヒストグラムを取る(pass 3)
「_calc_colour_hist」と「_calc_texture_hist」について見ていきます。
2-4-1. 色のヒストグラム
「_calc_colour_hist」について。チャンネル単位でヒストグラムを取っています。ここでimgは対応するRegionのピクセルで、HSV色空間です。
def _calc_colour_hist(img):
"""
calculate colour histogram for each region
the size of output histogram will be BINS * COLOUR_CHANNELS(3)
number of bins is 25 as same as [uijlings_ijcv2013_draft.pdf]
extract HSV
"""
BINS = 25
hist = numpy.array([])
for colour_channel in (0, 1, 2):
# extracting one colour channel
c = img[:, colour_channel]
# calculate histogram for each colour and join to the result
hist = numpy.concatenate(
[hist] + [numpy.histogram(c, BINS, (0.0, 255.0))[0]])
# L1 normalize
hist = hist / len(img)
return hist
HSVのチャンネルごとにヒストグラムを取ってくっつけているというのはなんとなくわかりますが、そもそもnp.histogramという関数が普段あまり使わないのでなんだかよくわかりません。np.histogramの部分だけ簡単な例にしてみると、
import skimage
import numpy as np
def image_histogram():
img = skimage.data.astronaut()
hists = []
for i in range(img.shape[-1]):
print(np.histogram(img[:,:,i], 10, (0.0, 255.0)))
if __name__ == "__main__":
image_histogram()
出力は、
(array([46243, 10944, 9481, 11914, 17199, 15791, 25332, 45602, 59968,
19670], dtype=int64), array([ 0. , 25.5, 51. , 76.5, 102. , 127.5, 153. , 178.5, 204. ,
229.5, 255. ]))
(array([66383, 14683, 16687, 26382, 29440, 16311, 27652, 38193, 20005,
6408], dtype=int64), array([ 0. , 25.5, 51. , 76.5, 102. , 127.5, 153. , 178.5, 204. ,
229.5, 255. ]))
(array([73679, 21874, 29250, 22768, 11976, 14541, 31133, 33826, 15727,
7370], dtype=int64), array([ 0. , 25.5, 51. , 76.5, 102. , 127.5, 153. , 178.5, 204. ,
229.5, 255. ]))
これはRGBの場合ですが、各チャンネルのヒストグラムの(棒の高さ, 対応するx座標)の順で返ってきているのがわかります。x座標はBINS(この例では10)と、値域(この例では0~255)が変わらない限り一定なので、1番目の返り値だけ取ればいいことになります。
くどいかもしれませんが、一般的なカラーヒストグラムを作ってみましょう。
import skimage
import numpy as np
import matplotlib.pyplot as plt
def image_histogram():
img = skimage.data.chelsea()
fig, ax = plt.subplots(2, 2, figsize=(8, 8))
ax[0][0].imshow(img)
ax[0][0].set_title("Original")
for i in range(img.shape[-1]):
y, x = np.histogram(img[:,:, i], 100, (0.0, 255.0))
ax[(i + 1) // 2][(i + 1) % 2].bar(x[:-1], y, width=2.0)
ax[(i + 1) // 2][(i + 1) % 2].set_title(["R", "G", "B"][i])
plt.show()
if __name__ == "__main__":
image_histogram()
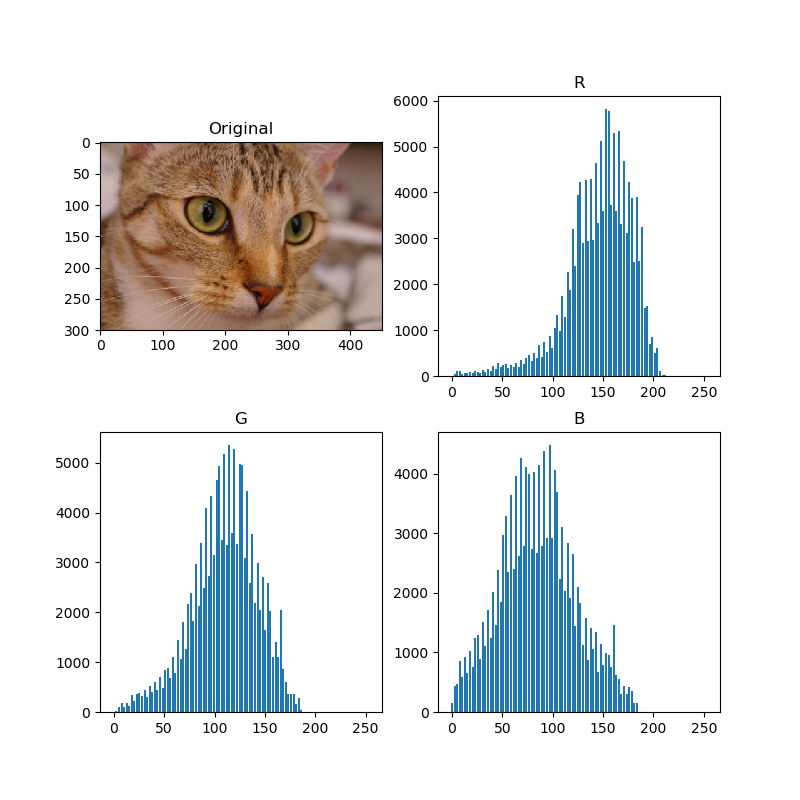
よく見るタイプのヒストグラムができました。Selective Searchではヒストグラムをピクセル数で標準化しています。
2-4-2. テクスチャ勾配のヒストグラム
色のヒストグラムと同様に、LBP(テクスチャ勾配)も同様にヒストグラムを作ります。GitHubのコードからです。
def _calc_texture_hist(img):
"""
calculate texture histogram for each region
calculate the histogram of gradient for each colours
the size of output histogram will be
BINS * ORIENTATIONS * COLOUR_CHANNELS(3)
"""
BINS = 10
hist = numpy.array([])
for colour_channel in (0, 1, 2):
# mask by the colour channel
fd = img[:, colour_channel]
# calculate histogram for each orientation and concatenate them all
# and join to the result
hist = numpy.concatenate(
[hist] + [numpy.histogram(fd, BINS, (0.0, 1.0))[0]])
# L1 Normalize
hist = hist / len(img)
return hist
やっていることは色のヒストグラムと同じです。RGB画像の各チャンネル単位のLBPについて、ヒストグラムを取っています。
3. Neighborの作成
ヒストグラムベースの特徴量を作ったら、重なっているRegionのペアを列挙しましょう。これはコードを見るのが早いです。GitHubのコードから。
def _extract_neighbours(regions):
def intersect(a, b):
if (a["min_x"] < b["min_x"] < a["max_x"]
and a["min_y"] < b["min_y"] < a["max_y"]) or (
a["min_x"] < b["max_x"] < a["max_x"]
and a["min_y"] < b["max_y"] < a["max_y"]) or (
a["min_x"] < b["min_x"] < a["max_x"]
and a["min_y"] < b["max_y"] < a["max_y"]) or (
a["min_x"] < b["max_x"] < a["max_x"]
and a["min_y"] < b["min_y"] < a["max_y"]):
return True
return False
R = list(regions.items())
neighbours = []
for cur, a in enumerate(R[:-1]):
for b in R[cur + 1:]:
if intersect(a[1], b[1]):
neighbours.append((a, b))
return neighbours
regionsというのはR(dict形式)です。全てのRから2つのRegionの組み合わせを列挙し、重なっているペアをどんどんappendしていくという単純なものです。intersectは読んで字の如く、2つの領域が重なっているかどうかを判定する関数です。
4. 全てのNeighborに対し、Region同士の類似度を計算
3で作ったNeighborのリストの中身は、(a, b)という2つのRegionからなるので、(a, b)の類似度を計算しておきます。計算した結果をSという変数に格納します。
S = {}
for (ai, ar), (bi, br) in neighbours:
S[(ai, bi)] = _calc_sim(ar, br, imsize)
この「_calc_sim」という計算は次のようになります。
def _sim_colour(r1, r2):
"""
calculate the sum of histogram intersection of colour
"""
return sum([min(a, b) for a, b in zip(r1["hist_c"], r2["hist_c"])])
def _sim_texture(r1, r2):
"""
calculate the sum of histogram intersection of texture
"""
return sum([min(a, b) for a, b in zip(r1["hist_t"], r2["hist_t"])])
def _sim_size(r1, r2, imsize):
"""
calculate the size similarity over the image
"""
return 1.0 - (r1["size"] + r2["size"]) / imsize
def _sim_fill(r1, r2, imsize):
"""
calculate the fill similarity over the image
"""
bbsize = (
(max(r1["max_x"], r2["max_x"]) - min(r1["min_x"], r2["min_x"]))
* (max(r1["max_y"], r2["max_y"]) - min(r1["min_y"], r2["min_y"]))
)
return 1.0 - (bbsize - r1["size"] - r2["size"]) / imsize
def _calc_sim(r1, r2, imsize):
return (_sim_colour(r1, r2) + _sim_texture(r1, r2)
+ _sim_size(r1, r2, imsize) + _sim_fill(r1, r2, imsize))
色、テクスチャ、サイズ、共通要素の4つの類似度から計算します。imsizeは画像全体の縦×横の値(面積)を表します。r1, r2のsizeは各Regionの面積です。
色、テクスチャのようにヒストグラムベースの類似度の場合は、2つのヒストグラムの各棒(bin)の最小値の和を取っています。完全に同一のヒストグラムなら最小値の和は、自身のヒストグラムの和と同じになります(標準化しているので1)。
サイズ(sim_size)と共通要素(sim_fill)は似たようなもので、共通要素のほうがオーバーラップしている面積を加味しています。
5. Hierarchal Search
これがSelective SearchのキーとなるHierarchal Searchの部分です。4.で計算した類似度のdict、Sを使います。次のようなアルゴリズムです。
- Sが空になるまでループ
- 最も高い類似度のペアを取る
- 該当する領域をマージする(Bounding Boxをたばねるのと同じ)
- マージした2つの領域をいずれかに含むペアをSから削除
- 新しい領域に対して類似度を計算
Hierarchal Searchのやっていることは「類似度が高いもの同士を束ねる」ということです。コードは次のようになります。GitHubのコードより
# hierarchal search
while S != {}:
# get highest similarity
i, j = sorted(S.items(), key=lambda i: i[1])[-1][0]
# merge corresponding regions
t = max(R.keys()) + 1.0
R[t] = _merge_regions(R[i], R[j])
# mark similarities for regions to be removed
key_to_delete = []
for k, v in list(S.items()):
if (i in k) or (j in k):
key_to_delete.append(k)
# remove old similarities of related regions
for k in key_to_delete:
del S[k]
# calculate similarity set with the new region
for k in [a for a in key_to_delete if a != (i, j)]:
n = k[1] if k[0] in (i, j) else k[0]
S[(t, n)] = _calc_sim(R[t], R[n], imsize)
Sは計算結果のキャッシュで、Regionを束ねるごとにSが減っていくのに対し、Rが束ねたものでどんどん積み重なっていくという構造です。最終的にRのアイテムを返します。
途中の「_merge_regions」のやっているのはBounding Boxを束ねるのと同じで、
def _merge_regions(r1, r2):
new_size = r1["size"] + r2["size"]
rt = {
"min_x": min(r1["min_x"], r2["min_x"]),
"min_y": min(r1["min_y"], r2["min_y"]),
"max_x": max(r1["max_x"], r2["max_x"]),
"max_y": max(r1["max_y"], r2["max_y"]),
"size": new_size,
"hist_c": (
r1["hist_c"] * r1["size"] + r2["hist_c"] * r2["size"]) / new_size,
"hist_t": (
r1["hist_t"] * r1["size"] + r2["hist_t"] * r2["size"]) / new_size,
"labels": r1["labels"] + r2["labels"]
}
return rt
という操作を行っています。ヒストグラムの統合が単純な和でできるのは面白いですね。
そして最後に束ねられたRegionがたくさん追加されたRについて、
regions = []
for k, r in list(R.items()):
regions.append({
'rect': (
r['min_x'], r['min_y'],
r['max_x'] - r['min_x'], r['max_y'] - r['min_y']),
'size': r['size'],
'labels': r['labels']
})
return img, regions
とすることでSelective Searchの結果となります。
Selective Searchを動かしてみる
「四の五の言わずにSelective Searchを動かしてみなさいよ」という声が出そうなので早速試してみましょう。
import skimage
from selectivesearch import selective_search
from PIL import Image, ImageDraw
import matplotlib.pyplot as plt
def selective_search_sample():
img = skimage.data.astronaut()
img_label, regions = selective_search(img, scale=500, sigma=0.9, min_size=500)
with Image.fromarray(img) as img:
draw = ImageDraw.Draw(img)
for r in regions:
draw.rectangle(r["rect"], outline="red", width=1)
plt.imshow(img)
plt.show()
if __name__ == "__main__":
selective_search_sample()
見やすくするための少しmin_sizeを大きく取っています。結果は以下の通り。
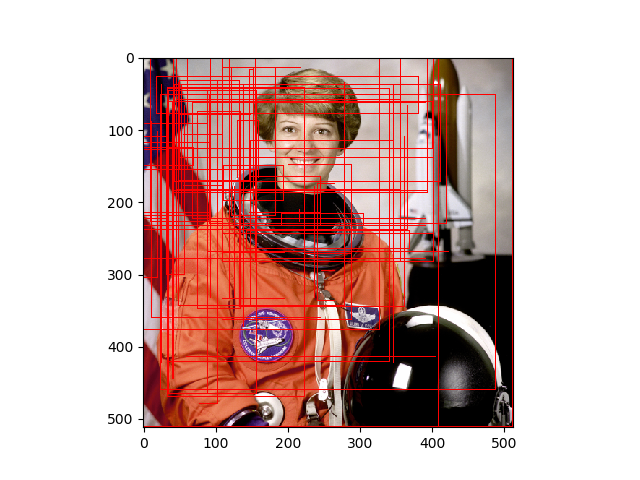
これだけ苦労した割に結果が微妙な気がしなくもないですが、まぁ古いアルゴリズムなので仕方ない。ただ、Selective Searchは「教師なし」だということを割り引いて考えるべきだと思います。後続の物体検出のモデルが、Selective Searchのような矩形選択をニューラルネットワークに組み込み、学習ベースにしているので、正直精度はあんまりよくないよということでしょうか。
オリジナルのRCNNではSelective Searchで得られたRegion Proposalに対し、画像分類をかけることで、物体検出を実践しています。
かなり特徴量の抽出がアドホックで、Regionの統合の部分がかなり重い(ここが非常にネック)なので、コミコミでニューラルネットワークにやらせるモデルに取って代わられるというのは当たり前のような感じがします。
まとめ
普段あまりちゃんと語られることのないSelective Searchですが、この記事ではソースコードを追って中で何をやっているのか見てきました。
Selective Searchを物体検出のモデルに組み込むのには微妙なので、これを追っても得られるものは少ないかと思いますが、物体検出の用語として出てくるSelective Search、Region Proposalの関係は抑えられたのではないかなと思います。
Shikoan's ML Blogの中の人が運営しているサークル「じゅ~しぃ~すくりぷと」の本のご案内
技術書コーナー
北海道の駅巡りコーナー

