統計学や機械学習で使われる分散共分散行列、相関行列とグラム行列の関係

TensorFlowなど分散共分散行列の計算関数が用意されていない場合は、分散共分散行列や相関行列を計算する際に自分で関数を定義しなければいけません。そこでグラム行列から、分散共分散行列、相関行列と派生させて計算する方法を理論を中心に見ていきます。
目次
きっかけは主成分分析を使ったPCA Color Augmentation
なぜ自分がTensorFlowで分散共分散行列の計算が必要になったかということですが、Data Augmentation用に「PCA Color Augmentation(Qiitaで書きました)」が必要になったからです。「Data AugmentationならNumpyで書けばよくね?」と思われるかもしれませんが、実はNumpyで書くと分散共分散行列の計算がボトルネックになって訓練速度が遅く(1.5倍~2倍レベル)なってしまいました。これはPCA Color Augmentationの記事ではないので詳細は別の機会にしますが、ちょっとCPU(Numpy)でやらせるにはハードな行列計算をGPUでブーストできるTensorFlowのレイヤーで定義しようというのがきっかけです。
TensorFlowにはcov関数がない
分散共分散行列の計算は、Numpyではnp.cov()という関数を使えば一発で計算してくれます。例えばIrisデータセットのカラム間の共分散を計算するコードは次のとおりです。
from sklearn.datasets import load_iris
import numpy as np
(iris_X, iris_y) = load_iris(return_X_y=True)
covmat = np.cov(iris_X, rowvar=False)
print(covmat)
#[[ 0.68569351 -0.03926846 1.27368233 0.5169038 ]
# [-0.03926846 0.18800403 -0.32171275 -0.11798121]
# [ 1.27368233 -0.32171275 3.11317942 1.29638747]
# [ 0.5169038 -0.11798121 1.29638747 0.58241432]]
今回はカラム(Irisだったらガクの長さや花弁の幅といった列の方向)間で集計しましたが、Numpyでは列の方向と行の方向の両方で集計できるようになっています。引数の「rowvar=False」は「行方向ではない、つまり列方向での分散を計算するよ」という意味です。
さて、TensorFlowでは2018年10月時点でnp.covに相当する、分散共分散行列の計算関数がありません。先程のPCA Color Augmentationだけじゃなくて、レイヤーの途中で主成分分析やカーネル法で多分使うと思うんですがなぜないんでしょうね。Back Propの定義の都合上なのかな(適当な想像)。
グラム行列と分散共分散行列の関係
分散共分散行列を数式で見てみましょう。分散共分散行列にはいくつか公式のような重要な性質があって、
$$Cov(X)=E[X^TX] – \mu^T\mu \tag{1}$$
で表されます。ここでCov(X)は分散共分散行列を表します。$E[\cdot]$は期待値を表す関数。$\mu$は平均のベクトルです。サイトによっては(Wikipediaもそうですが)、
$$Cov(X)=E[XX^T] – \mu\mu^T \tag{2}$$
とかける順序を逆に書いているサイトも多いです。もちろんどっちが正しくてどっちが間違いということはなくて、Xの定義によりけりなんですよね。例えば今回のIrisの場合、
print(iris_X.shape)
# (150, 4)
となり、Xは150×4の行列であることがわかります。(2)式の計算方法で計算すると、期待値の中身は150×4の行列と4×150の行列の積になるので、150×150の行列になってしまいます。(1)式の計算方法で計算すると、4×150と150×4の行列の積なので、期待された4×4の行列ができます。数学のページではないので、Xの行列の定義とかは厳密にしませんが(ぶっちゃけ自分がそういうのできるほど知識がない)、状況に応じて変わるよということを言いたかっただけです。ちょうど、np.covのrowvarをTrueとするか、Falseとするかのような違いです。(2)の式も間違いではないですが、今回の記事では(1)の式を使います。
さて、(1)の式ですが、もしXが平均で引かれていたらどうでしょうか?ここで注意したいのが、平均で引く操作は 標準化や正規化(どちらも英語ではnormalization)と言われる操作とは異なることです。後で説明しますが、データを標準化してグラム行列を計算すると相関行列となります。分散共分散行列を出したいときは標準偏差で割るのではなく平均だけ引けばいいです。
Xが系列間の平均で引かれていた、つまり平均補正済みとしましょう。このときデータの系列間の平均は0になるので、
$$\mu^T\mu=0$$
となります。つまり、Xが平均補正済みだとしたら分散共分散行列は、
$$Cov(X)=E[X^TX]$$
という簡単な式になります。さて、期待値の中身は前回の記事で見たようにグラム行列なので、こういうが言えます。「XがXの系列間の平均で引かれていたら、分散共分散行列の導出はグラム行列の期待値を取ればよい」
本当にそうなるかNumpyで確認していきましょう。
平均で引かれていたら、分散共分散行列=グラム行列の期待値
まずは前回のおさらい。グラム行列とは行列$X$に対して次のような行列積計算を行って得られた行列のことです。
$$X^T X$$
Numpyで計算するときはランク2のテンソルである行列の場合は、np.dot(X.T, X)で計算できます。
import numpy as np
matrix = np.arange(4).reshape(2,2)
gram = np.dot(matrix.T, matrix)
print("gram : ")
print(gram)
#gram :
#[[ 4 6]
# [ 6 10]]
例としてはIrisデータセットをそのまま使います。Iris_Xを平均で引きグラム行列の期待値を取ったら、本当にnp.cov()で計算できた分散共分散行列と等しくなるか確認します。
from sklearn.datasets import load_iris
import numpy as np
(iris_X, iris_y) = load_iris(return_X_y=True)
# サンプル数(後で期待値の計算に使う)
n_sample = iris_X.shape[0]
print(n_sample) # 150
# 系列の平均
column_mean = np.mean(iris_X, axis=0, keepdims=True)
print(column_mean.shape) # (1, 4)
# 平均で引く
iris_X_meanadj = iris_X - column_mean
print(iris_X_meanadj.shape) # (150, 4)←変わっていない
# 平均で引いたグラム行列
gram_meanadj = np.dot(iris_X_meanadj.T, iris_X_meanadj)
# グラム行列の期待値
gram_meanadj_exp = gram_meanadj / n_sample
print("平均で引く→グラム行列の期待値")
print(gram_meanadj_exp)
# np.covによる分散共分散行列
print("分散共分散行列")
print(np.cov(iris_X, rowvar=False))
出力は次の通りです。小数第3位ぐらいになってくると誤差で若干変わっていますが、だいたい同じ結果を返しているのが確認できます。
追記:誤差ではなくNumpyのcovが不偏分散で計算しているからだそうです。N-1と計算するとあいます。
平均で引く→グラム行列の期待値
[[ 0.68112222 -0.03900667 1.26519111 0.51345778]
[-0.03900667 0.18675067 -0.319568 -0.11719467]
[ 1.26519111 -0.319568 3.09242489 1.28774489]
[ 0.51345778 -0.11719467 1.28774489 0.57853156]]
分散共分散行列
[[ 0.68569351 -0.03926846 1.27368233 0.5169038 ]
[-0.03926846 0.18800403 -0.32171275 -0.11798121]
[ 1.27368233 -0.32171275 3.11317942 1.29638747]
[ 0.5169038 -0.11798121 1.29638747 0.58241432]]
分散共分散行列と相関行列の関係、グラム行列と相関行列の関係
さきほど少し触れた平均で引くだけでなく標準偏差で割られていた場合、つまりデータが標準化されていた場合はどうなるか見てましょう。結論からいうと、グラム行列の期待値は相関行列になります。
相関行列というと統計やっていた方ならあーと思い浮かぶと思います。系列間のパラメーターの相関を見るときにとても便利な行列です。例えばIrisの相関行列は次のようになります。
[[ 1. -0.10936925 0.87175416 0.81795363]
[-0.10936925 1. -0.4205161 -0.35654409]
[ 0.87175416 -0.4205161 1. 0.9627571 ]
[ 0.81795363 -0.35654409 0.9627571 1. ]]
対角成分は同一系列の相関を取ったものなので必ず1になります。データの傾向見る際は便利なのでぜひ活用してみてください。
相関行列と分散共分散行列は別物ではなく、相関行列が分散共分散行列の特殊な場合と考えるほうが自然です。相関行列の定義は、これは相関係数の定義ですが、系列$X_i$と$X_j$の相関係数$\rho_{ij}$は、
$$\rho_{ij}=\frac{\sigma_{X_iX_j}}{\sigma_{X_i}\sigma_{X_j}} $$
で表されます。ここで分子は$X_i$と$X_j$の共分散、分母はそれぞれの分散を表します。これを行列表記にしてみましょう。今$\Sigma$を分散共分散行列とし、$P$を相関行列とします。系列数がN個あるものとし(Irisの例ではN=4です)、$\Sigma$と$P$ともにN×N行列で表されます。また、分散共分散行列の対角成分を$\sigma$で取り出します。本来はこの対角成分はベクトルですが、以下のような1×Nの列行列で定義します。
$$\sigma = [\sigma_{X_1}, \cdots, \sigma_{X_i}, \cdots, \sigma_{X_N}]$$
括弧の中身は要素ごとの分散ですね。で、これは本来の数学の計算ではないのですが、Pythonではできるブロードキャスティングを使った計算で、$\sigma$をsigmaという変数に入れ、次のコードで求められる行列を$S$とします。
S = np.sqrt(sigma.T * sigma)
これは相関係数の定義にある分母の値を行列で書き直したものにすぎません。この$S$という行列が定義できれば、相関行列$P$は分散共分散行列$\Sigma$を用いて次のように表されます。
$$P=\frac{\Sigma}{S} $$
ここでの演算は要素間の割り算です(もう少し厳密に言うならアダマール積の割り算版)。つまり、このSの行列の成分が全て1になれば$P=\Sigma$という式が成立します。ちなみにもっと厳密な数学の定義は、高校数学の美しい物語にある「相関行列の定義と分散共分散行列との関係」をご覧ください。なるほど、こう書くのかと思いました。
行列Sの成分が全て1になるということは、Xの系列間の分散が全て1になるということなので、「系列間の標準偏差で割る」という補正をしていた場合は、分散共分散行列=相関行列となります。さらに分散共分散行列については、「系列間の平均で引く」という補正をしていた場合は、分散共分散行列=グラム行列の期待値となります。
つまり三段論法的な発想により、「データを標準化していたら」グラム行列の期待値は相関行列と等しくなる。という結論が出ます。これを実際のデータで確認してみます。
標準化していたら、相関行列=分散共分散行列=グラム行列の期待値
Irisデータで確かめる
標準化済みのグラム行列の期待値と、分散共分散行列と、標準化していないときの相関行列が等しくなるのを確認します。
from sklearn.datasets import load_iris
import numpy as np
(iris_X, iris_y) = load_iris(return_X_y=True)
# サンプル数(後で期待値の計算に使う)
n_sample = iris_X.shape[0]
print(n_sample) # 150
# 系列の平均
column_mean = np.mean(iris_X, axis=0, keepdims=True)
print(column_mean.shape) # (1, 4)
# 系列の標準偏差
column_sd = np.std(iris_X, axis=0, keepdims=True)
print(column_sd.shape) # (1, 4)
# データの標準化
iris_X_normalized = (iris_X - column_mean) / column_sd
# グラム行列の期待値
gram_exp = np.dot(iris_X_normalized.T, iris_X_normalized) / n_sample
print("標準化済みグラム行列の期待値")
print(gram_exp)
# 標準化済みのときの分散共分散行列
cov = np.cov(iris_X_normalized, rowvar=False)
print("標準化済みの分散共分散行列")
print(cov)
# 実際の相関行列
corr = np.corrcoef(iris_X, rowvar=False)
print("実際の相関行列")
print(corr)
結果は以下の通りです。
標準化済みグラム行列の期待値
[[ 1. -0.10936925 0.87175416 0.81795363]
[-0.10936925 1. -0.4205161 -0.35654409]
[ 0.87175416 -0.4205161 1. 0.9627571 ]
[ 0.81795363 -0.35654409 0.9627571 1. ]]
標準化済みの分散共分散行列
[[ 1.00671141 -0.11010327 0.87760486 0.82344326]
[-0.11010327 1.00671141 -0.42333835 -0.358937 ]
[ 0.87760486 -0.42333835 1.00671141 0.96921855]
[ 0.82344326 -0.358937 0.96921855 1.00671141]]
実際の相関行列
[[ 1. -0.10936925 0.87175416 0.81795363]
[-0.10936925 1. -0.4205161 -0.35654409]
[ 0.87175416 -0.4205161 1. 0.9627571 ]
[ 0.81795363 -0.35654409 0.9627571 1. ]]
分散共分散行列がちょっと誤差ありますが、グラム行列の期待値と実際の相関行列は完全に同じ値を返していますね。きっとnp.corrcoefの実装がこんなのなんでしょう。
一般の分散共分散行列から相関行列を求める方法
さて、補足ですが、標準化していない一般の分散共分散行列から相関行列を求める方法をコードで確認しておきましょう。
from sklearn.datasets import load_iris
import numpy as np
(iris_X, iris_y) = load_iris(return_X_y=True)
# 分散共分散行列
cov = np.cov(iris_X, rowvar=False)
# 分散共分散行列の対角成分
cov_diag = np.expand_dims(np.diag(cov), axis=0)
# 対角成分とその転置のelementwise積
S = np.sqrt(cov_diag.T * cov_diag)
# 手動で求めた相関行列
corr_manual = cov / S
print("分散共分散行列から求めた相関行列")
print(corr_manual)
# 実際の相関行列
corr = np.corrcoef(iris_X, rowvar=False)
print("実際の相関行列")
print(corr)
やっていることは先程述べたこととをコードに書き換えたものです。
分散共分散行列から求めた相関行列
[[ 1. -0.10936925 0.87175416 0.81795363]
[-0.10936925 1. -0.4205161 -0.35654409]
[ 0.87175416 -0.4205161 1. 0.9627571 ]
[ 0.81795363 -0.35654409 0.9627571 1. ]]
実際の相関行列
[[ 1. -0.10936925 0.87175416 0.81795363]
[-0.10936925 1. -0.4205161 -0.35654409]
[ 0.87175416 -0.4205161 1. 0.9627571 ]
[ 0.81795363 -0.35654409 0.9627571 1. ]]
一致しているのを確認できましたね。これで分散共分散行列、相関行列をマスターできました。
グラム行列、分散共分散行列、相関行列の関係のまとめ
今までの議論をまとめると次の図になります。これを見るともう少しすっきり理解できるのではないでしょうか。
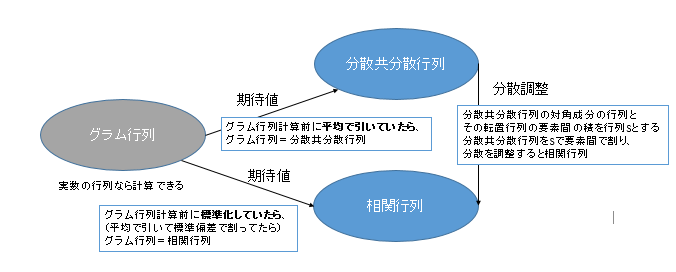
今、実数の行列の話のみ考えるとしましょう。グラム行列というのはとても広い考え方で、どんな行列を取ってこようがその結果はみんなグラム行列と呼びます。分散共分散行列、相関行列はおおよその行列で計算できますが、スケールだったり対角要素だったりだんだん縛りが多くなり、より狭い概念となっていきます。
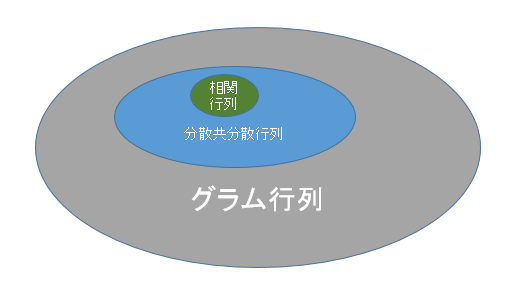
分散共分散行列はグラム行列より狭い概念で、「グラム行列計算前に平均で引いていたら」そのグラム行列の期待値が、分散共分散行列と等しくなります。相関行列はもっと狭い概念で、「グラム行列計算前に標準化していたら」、グラム行列の期待値が相関行列と等しくなります。分散共分散行列と相関行列の関係は、先程見たような分散の調整を行ったものですが、やはり相関行列のほうが狭い概念です。
期待値操作や、スケール調整が入るため、必ずしもこのような包含図が正しいとは限りませんが、漠然とした理解ではこのような図になります。実際に実装するときはこれだけわかってれば大丈夫です。
TensorFlowへの実装へのまとめ
これまで、グラム行列、分散共分散行列、相関行列への関係を見てきましたが、理解できたでしょうか?
分散共分散行列、相関行列の関数がないときは、前回みたような方法でグラム行列を計算すればよいことがわかりました。あとはデータの標準化次第で、分散共分散行列になるか、相関行列になるかが決まるというわけです。次回は実際にTensorFlowで実装してみます。
次回:TensorFlow/Kerasでの分散共分散行列・相関行列、テンソル主成分分析の実装
https://blog.shikoan.com/tensorflow-varcov-pca/
Shikoan's ML Blogの中の人が運営しているサークル「じゅ~しぃ~すくりぷと」の本のご案内
技術書コーナー
北海道の駅巡りコーナー

