論文まとめ：Deep Spectral Methods: A Surprisingly Strong Baseline for Unsupervised Semantic Segmentation and Localization

---

• タイトル：Deep Spectral Methods: A Surprisingly Strong Baseline for Unsupervised Semantic Segmentation and Localization
• カンファ：CVPR2022
• 著者：Luke Melas-Kyriazi, Christian Rupprecht, Iro Laina, Andrea Vedaldi
• 所属：オックスフォード大学
• 論文：https://arxiv.org/abs/2205.07839
• プロジェクトページ：https://lukemelas.github.io/deep-spectral-segmentation/
• デモ：https://huggingface.co/spaces/lukemelas/deep-spectral-segmentation

ざっくりいうと

• 自己教師あり学習モデルの中間層の値を使い、教師なしで物体検出やセグメンテーションを行う研究
• スペクトルグラフ理論をベースとし、アフィン行列の固有ベクトルを解析する。セグメンテーションでは追加でクラスタリングを行い、擬似ラベルを獲得する
• 従来の教師なしの検出やセグメンテーションを大きくアウトパフォームしSoTA。Mattingにも応用可能

背景

• アノテーションコストの問題がある。特にセグメンテーションや医用画像ではコストが高価
• 画像分解をグラフ分割問題として考える。伝統的なスペクトル分割法から着想を得ている。
  • 具体的には、自己教師ありネットワークから特徴アフィン行列のラプラシアンの固有ベクトルを調べる
• 固有ベクトルは既に画像を意味のあるセグメントに分解しており、シーン内の物体の位置特定に容易に利用できた

手法

コードによるざっくりとした説明

いきなりグラフ理論を出してもわからないので、中間層の値から固有ベクトルを求める（後述の$W_{feat}$）コードの解説。実装はかなり単純。

中間層の値をとって、TransformerのMulti Head Attention-likeにReshapeする。コードより

model.get_intermediate_layers(images)[0].squeeze(0)
output_qkv = feat_out["qkv"].reshape(B, T, 3, num_heads, -1 // num_heads).permute(2, 0, 3, 1, 4) # [3, B, N, T, -1//N]
output_dict['k'] = output_qkv[1].transpose(1, 2).reshape(B, T, -1)[:, 1:, :]
# [B, N, T, -1//N] -> [B, T, N, -1//N] -> [B, T, N] -> [B, T-1, N]

特徴量のアフィン行列（グラム行列）をとって、固有ベクトルと固有値を求める。

# Load affinity matrix
feats = data_dict[which_features].squeeze().cuda()
if normalize:
    feats = F.normalize(feats, p=2, dim=-1)

# Eigenvectors of affinity matrix
if which_matrix == 'affinity_torch':
    W = feats @ feats.T
    if threshold_at_zero:
        W = (W * (W > 0))
    eigenvalues, eigenvectors = torch.eig(W, eigenvectors=True)
    eigenvalues = eigenvalues.cpu()
    eigenvectors = eigenvectors.cpu()

これが基本。次に理論的な背景。

理論的な背景

（理論は難しいので飛ばしていいです）

この論文はスペクトルグラフ理論がベースになっている。

• 重みつき無向グラフ$G=(V, E)$と、隣接行列$W={w(u,v):(u,v)\in E}$がある。$V$は頂点、$E$はエッジ
• ラプラシアン行列$L$は、$L=D-W$または$L=D^{-1/2}(D-W)D^{-1/2}$（正規化したケース）
• ここで$D$は対角行列で、対角成分が行単位の$W$の和

ラプラシアン行列は特に次の性質を持っている。$x\in\mathbb{R}^n, n=|V|$

$$x^TLx = \sum_{(u,v)\in E} w(u, v)\cdot(x(u)-x(v))^2$$

直感的にはこの二次形式は、グラフ$G$の関数$x$の滑らかさを表している。$x$が$G$に対して滑らかであれば、$u$が$v$に似ているときはいつでも$x(u)$は$x(v)$に似ている。類似度は重み$w(u, v)$で定量化される。

スペクトルグラフ理論のアプローチで、$L$の固有ベクトル$y_i$は、$G$上の関数の直交基底にまたがるもので、上記の意味で最も滑らかな直交基底で、

$$y_i = \arg\min_{|x|=1, x\perp y<i} x^TLx$$

ここで$y_0=\mathbb{1}\in\mathbb{R}^n$で、固有値$\lambda_i$は$0=\lambda_0 \leq \lambda_1 \leq \cdots \leq \lambda_{n-1}$。これはスペクトルグラフ理論では「Courant-Fischerの定理」と呼ばれている。

$G$上の関数を、グラフのラプラシアンの固有ベクトルをもとにして表現できる。これを、画像セグメンテーションに対応すると、

• ノード$G$：画像$I\in\mathbb{R}^MN$
• エッジの重み$E\in\mathbb{R}^{MN\times MN}$（ピクセル間のアフィン）
• 固有ベクトル$y\in\mathbb{R}^{MN}$はソフトな画像セグメントである

全体像

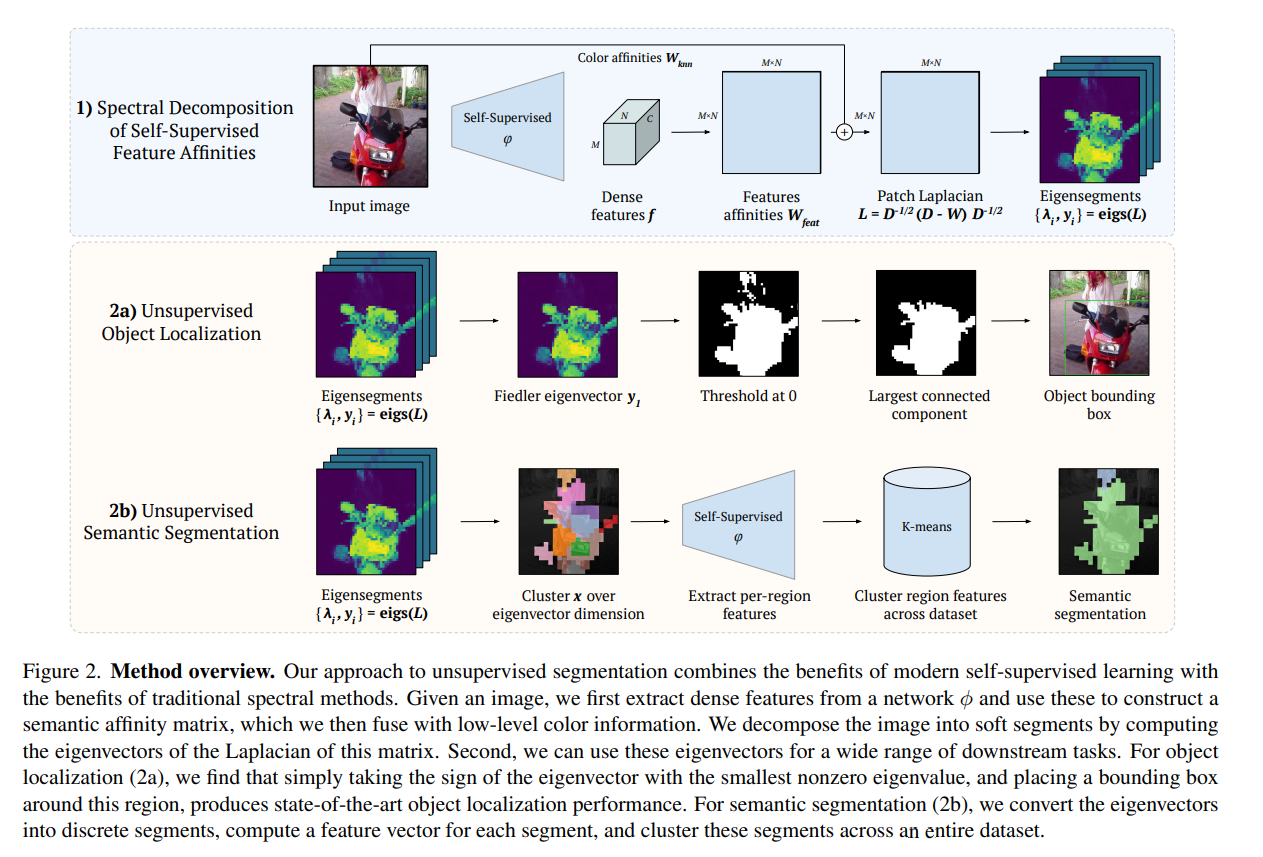
W_knn

中間層の値のほかに、入力画像をベースにした$W_{knn}$という特徴量を作る。これはImage Mattingの文脈から生まれたもの。入力画像をHSV色空間にして、

$$\psi(u))=\bigl(\cos(c_H),\sin(c_H),c_S,c_V,p_x,p_y \bigr)\in\mathbb{R}^5$$

ここで$c_H, c_S, c_V$はHSV色空間上の値で、$H$の色相だけ色相環なのでsin, cosをとっている。$p_x, p_y$は空間上の座標。次のようなknnベースの特徴量$W_{knn}$を作る。

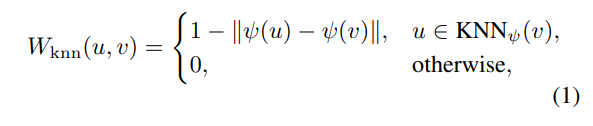
このアフィン行列は、オブジェクトの境界をシャープにするが、意味的な情報がない。そのため、特徴量ベースの$W_{feat}$も作る（先程コードで紹介したのがこれ）

意味的スペクトル分解（W_feat）

入力画像を$I\in\mathbb{R}^{3\times M\times N}$とする。ある中間層の特徴量を$f=\phi(I)\in\mathbb{R}^{C\times M/P\times N/P}$とする。ここで$P$はダウンサンプリング係数。

$$W_{feat} = ff^T \odot(ff^T>0)\in\mathbb{R}^{\frac{MN}{p^2}\times\frac{MN}{p^2}}$$

この$W_{feat}$という特徴は、意味的な情報を豊富に含んでいるが、低レベルの情報が失われている。これを$W_{knn}$から取り戻す。$W_{knn}$と$W_{feat}$は解像度が違うが、$W_{knn}$を中間解像度$M’\times N’$にダウンサンプリングして調整する。$M’=M/8, N’=N/8$が速度の維持と低レベル情報の両立ができると経験にわかっている。2つの重みつき平均和をとり

$$W=W_{feat}+\lambda_{knn}W_{knn}$$

モデル$\phi$を自己教師あり学習で訓練するのがポイントで（DINO-ViT-Baseを使用）、タスクごとに別途の教師データやファインチューニングが不要。

Object Localization

コード

• 論文では「Fiedler eigenvector y1」と書いてあるが、ただ最初の固有ベクトルをとっているだけに見える。
• 「Largest connected component」はskimage.measure.labelで計算

Object Segmentation

これはバイナリーのセグメンテーション（前景、背景）。Object Localizationと同様だが、$M’\times N’\to M\times N$へのアップサンプリング時に、Pairwise CRFが入っている。これはSimpleCRFというライブラリを使って実装している。コード

Semantic Segmentation

1. Object Localizationの要領で、セグメントごとに分割し、クラスタリング（1回目）を評価する
   • 最初のm個の固有ベクトル${y_1, \cdots, y_m}$に対して行う
   • クラスタリングは画像ごとに個別に行うため、画像ごとにインデックスがどのクラスに対応しているかの一貫性はない
2. セグメントごとの特徴ベクトルを計算する
3. 画像の集合に対してクラスタリング（2回目）を行い、画像ごとに異なったインデックスを全体で紐づける
   • これはセグメントごとの特徴量を、画像全体で計算する

→オプションとして、これを擬似ラベルとして自己教師あり学習をする。図のBaselineは自己教師あり学習なしの擬似ラベルだけ。Oursは自己教師あり学習を追加でしたもの。

擬似ラベルによる自己教師あり学習を追加したほうが、より洗練された推論結果になっている。

定量評価

Object Localization

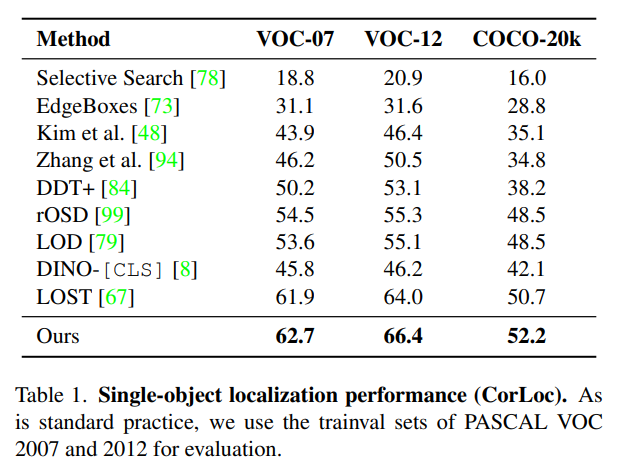
物体が1個だけなら教師なしでもかなり良好。指標はIoUが0.5以上のBoxの割合。

Segmentation

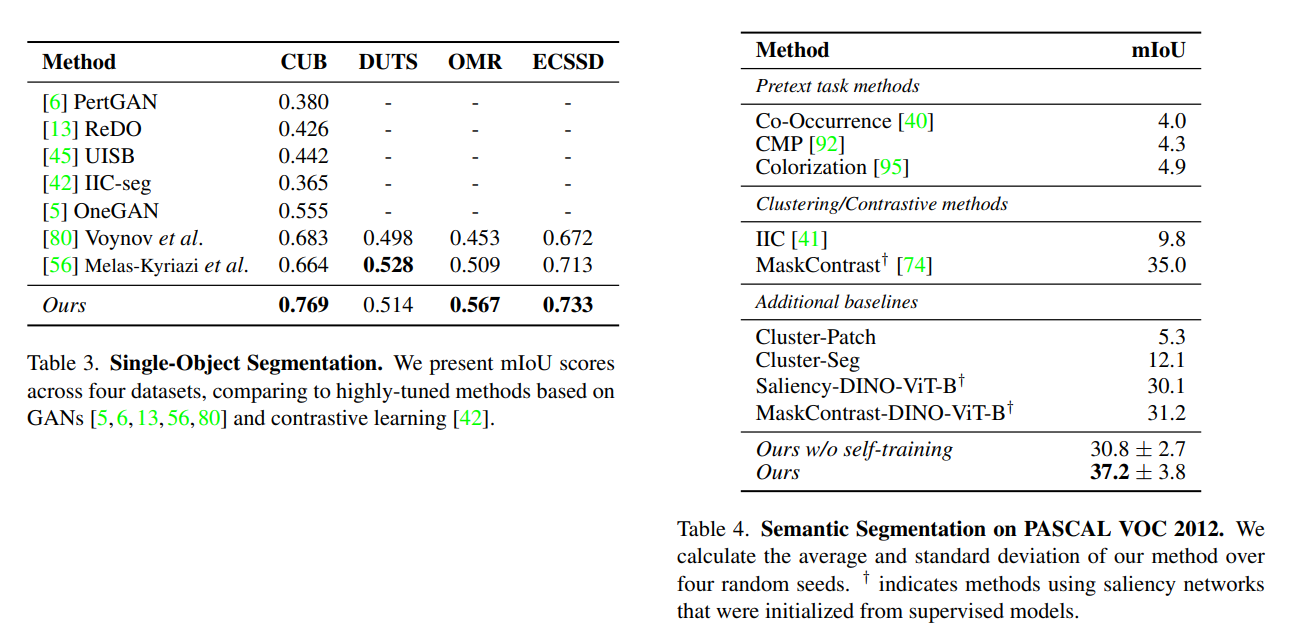
単一オブジェクトのセグメンテーションはかなり良好だが、複数クラスのセグメンテーションはまだまだ難易度が高い。

Mattingへの応用

単一オブジェクトのセグメンテーションはMatting問題でもあるので、この応用を検討している。Mattingへの応用は、小さな変更ででき、

• スペクトラルクラスタリングを中間層の縮小された解像度$M’, N’$で行うのではなく、画像の元解像度$M, N$で行う
• 計算量の都合上、$W_{feat}$を$1/16^2$にダウンサンプリングして使用するが、少量でも有効である

図の上が$W_{feat}$を使ったときの固有ベクトル、下が色情報だけの固有ベクトル。少量でも使ったときのほうが、意味情報をきちんととらえた固有ベクトルになっている（したがって最大の固有ベクトルをとればきちんとMattingしてくれる）

まとめと感想

• 教師なしで物体検出やセグメンテーションで、物体の数を絞れば十分な精度が出せるのが驚異的。自己教師あり学習だけでこれだけ出るのは驚いた。
• スペクトルグラフ理論は難しいが、基本は特徴量のアフィン行列とって固有ベクトル求めるだけの単純な実装。セグメンテーションになるとやや複雑なクラスタリングが入る
• Appendixに実装が詳細に載っており、コードも充実していてかなり親切な論文だと思った

---

---

Shikoan's ML Blogの中の人が運営しているサークル「じゅ～しぃ～すくりぷと」の本のご案内

---