PyTorchで行列(テンソル)積としてConv2dを使う

PyTorchではmatmulの挙動が特殊なので、思った通りにテンソル積が取れないことがあります。この記事では、基本的な畳み込み演算である「Conv2D」を使い、Numpyのドット積相当の演算を行うという方法を解説します。
目次
はじめに
PyTorchの変態コーディング技術です。多分。
画像のテンソルのチャンネル成分に対して処理をかけたいというのはときどき遭遇します。Keras(TensorFlowバックエンド)だとチャンネルが最後にあるので、4階テンソルに対して2×2行列をK.dotで掛けて終わりですが、PyTorchだとチャンネルが最後ではない(NCHWなので2番目)ので、かなり面倒です。
先に結論を言うと、この手のテンソル積を取りたいときは、torch.matmulなのですが、PyTorchのmatmulの挙動が相当特殊なので、自分では再現できませんでした。Torchのテンソルをpermute関数使って軸を逐一入れ替えて積を取るとかは一応できるのですが、それだとパフォーマンス面でちょっとどうなのかな?と思うわけです。
PyTorchの場合はいい方法見つけました。1×1畳み込みの計算が同じなのでConv2Dを使ってテンソル積を計算してしまうという方法です。Numpy、Keras、PyTorchの順に具体例で説明していきます。
具体例:色空間変換
画像の色空間を考えます。普段ピクセルのRGB値というときはRGB色空間ですが、輝度や色差といった情報を取り出したい場合は別の色空間に変換するのが便利です。ピクセル値は24ビットカラーでは0~255の整数ですが、RGB色空間では0~1の小数で考えます。一方で、YCrCb色空間は、Y(輝度)は0~1、CrCb(色差)は-0.5~0.5の小数で定義されます。
RGB色空間→YCrCb色空間への変換、あるいはその逆変換は行列積で計算できます。Wikipediaによれば
$$ \begin{bmatrix}Y\\Cr\\Cb\end{bmatrix} = \begin{bmatrix}0.299 & 0.587 & 0.114 \\ 0.5 & -0.418688 & -0.081312 \\ -0.168736 & -0.331264 & 0.5 \end{bmatrix} \begin{bmatrix}R\\G\\B\end{bmatrix}$$
$$\begin{bmatrix}R\\G\\B\end{bmatrix} = \begin{bmatrix}1 & 1.402 & 0 \\ 1 & -0.714136 & -0.344136 \\ 1 & 0 & 1.772\end{bmatrix}\begin{bmatrix}Y\\Cr\\Cb\end{bmatrix}$$
で表されます。本当にこんなんで正しいの?ということで、RGB→YCrCb→RGB、YCrCb→RGB→YCrCbの変換をしても元に戻る(行列積が単位行列になる)のを確認します。
import numpy as np
RGB2YCrCb = np.array([[0.299, 0.587, 0.114],
[0.5, -0.418688, -0.081312],
[-0.168736, -0.331264, 0.5]], np.float32)
YCrCb2RGB = np.array([[1, 1.402, 0],
[1, -0.714136, -0.344136],
[1, 0, 1.772]], np.float32)
print(np.dot(RGB2YCrCb, YCrCb2RGB))
print(np.dot(YCrCb2RGB, RGB2YCrCb))
結果は以下のようになります。
[[ 1.0000000e+00 1.3312457e-07 1.6485286e-07]
[ 0.0000000e+00 1.0000001e+00 7.5418632e-07]
[ 0.0000000e+00 -3.1320928e-07 9.9999982e-01]]
[[ 1.0000000e+00 -5.4178543e-07 5.7903833e-07]
[ 1.2339633e-07 1.0000001e+00 -1.7881393e-07]
[-1.8215839e-07 2.3836556e-07 1.0000000e+00]]
どちらも単位行列となりました(若干誤差はある)。確かに正しそうです。
Numpyで色空間変換
さて、色空間変換を画像に適用してみましょう。
こちらの記事からテスト用のカラーグラデーションを持ってきて使います。これを「color_bar.png」とします。

from PIL import Image
import numpy as np
RGB2YCrCb = np.array([[0.299, 0.587, 0.114],
[0.5, -0.418688, -0.081312],
[-0.168736, -0.331264, 0.5]], np.float32)
YCrCb2RGB = np.array([[1, 1.402, 0],
[1, -0.714136, -0.344136],
[1, 0, 1.772]], np.float32)
def numpy_version():
with Image.open("color_bar.png") as img:
rgb_array = np.asarray(img, np.float32) / 255.0
print("RGB original")
print(rgb_array.shape)
check_range(rgb_array)
print()
ycrcb_array = np.dot(rgb_array, RGB2YCrCb.T)
print("Coverted to YCrCb")
print(ycrcb_array.shape)
check_range(ycrcb_array)
print()
recon_array = np.dot(ycrcb_array, YCrCb2RGB.T)
print("Reconstrunction RGB")
print(recon_array.shape)
check_range(recon_array)
def check_range(img_array):
x =img_array.reshape(-1, img_array.shape[2])
mins = np.min(x, axis=0)
maxs = np.max(x, axis=0)
print("mins :", mins)
print("maxs :", maxs)
if __name__ == "__main__":
numpy_version()
先に全体のコードを貼ります。やっているのことは、画像を読み込む→RGB色空間のテンソルとして保存→YCrCb色空間に変換→RGB色空間に戻すということです。各処理の終わりにcheck_rangeという値域の確認用の関数を差し込んいます。これでRGB色空間は全て0~1、YCrCb色空間はYが0~1/CrCbが-0.5~0.5の範囲にあるということを確認します。
結果は次の通りになります。
RGB original
(800, 1280, 3)
mins : [0. 0. 0.]
maxs : [1. 1. 1.]
Coverted to YCrCb
(800, 1280, 3)
mins : [ 4.4705885e-04 -5.0000000e-01 -5.0000000e-01]
maxs : [1. 0.5 0.5]
Reconstrunction RGB
(800, 1280, 3)
mins : [-5.3644180e-07 -1.7881393e-07 -1.7881393e-07]
maxs : [1.0000006 1.0000002 1.0000002]
うまく行っています。YCrCbにすると2,3つ目の最小が-0.5, 最大が0.5になるのに対して、RGBに再度戻すと全て最小が0、最大が1に統一されていますね。
ここからがポイントなのですが、全ての変換計算はnp.dotというドット積の関数で計算しています。3階テンソルと2階テンソルの掛け算ですが、(800, 1200, 3)の最後の3に合わせて(3, 3)を掛けるという計算ですね。もし掛ける側が(3, 4)になったら、(800, 1200, 4)という出力になりますね。
ただし、変換式の定義がピクセル値を右からかけるのに対して、np.dotではピクセル値を左からかけているので、変換行列の転置操作が必要になります。
Kerasの場合
Kerasの場合はNumpyとほとんど変わりません。実際の画像処理では画像を複数まとめてミニバッチとして扱うことが多いので、np.expand_dimsで4階テンソルとして計算します。バッチサイズが1のミニバッチですね。
import keras.backend as K
import numpy as np
from PIL import Image
RGB2YCrCb = np.array([[0.299, 0.587, 0.114],
[0.5, -0.418688, -0.081312],
[-0.168736, -0.331264, 0.5]], np.float32)
YCrCb2RGB = np.array([[1, 1.402, 0],
[1, -0.714136, -0.344136],
[1, 0, 1.772]], np.float32)
def keras_version():
with Image.open("color_bar.png") as img:
rgb_array = np.asarray(img, np.float32) / 255.0
rgb_tensor = K.variable(np.expand_dims(rgb_array, axis=0))
print("RGB original")
print(rgb_tensor.shape)
check_range(rgb_tensor)
print()
ycrcb_tensor = K.dot(rgb_tensor, K.variable(RGB2YCrCb.T))
print("Coverted to YCrCb")
print(ycrcb_tensor.shape)
check_range(ycrcb_tensor)
print()
recon_tensor = K.dot(ycrcb_tensor, K.variable(YCrCb2RGB.T))
print("Reconstrunction RGB")
print(recon_tensor.shape)
check_range(recon_tensor)
def check_range(img_tensor):
img_array = K.eval(img_tensor)
x =img_array.reshape(-1, img_array.shape[3])
mins = np.min(x, axis=0)
maxs = np.max(x, axis=0)
print("mins :", mins)
print("maxs :", maxs)
if __name__ == "__main__":
keras_version()
np.dotをK.dotに置き換えればいいだけです。掛けられる側が3階テンソルだろうが、4階テンソルだろうが大丈夫です。以下のようになります。
RGB original
(1, 800, 1280, 3)
mins : [0. 0. 0.]
maxs : [1. 1. 1.]
Coverted to YCrCb
(1, 800, 1280, 3)
mins : [ 4.4705885e-04 -5.0000000e-01 -5.0000000e-01]
maxs : [1. 0.5 0.5]
Reconstrunction RGB
(1, 800, 1280, 3)
mins : [-5.3644180e-07 -1.7881393e-07 -1.7881393e-07]
maxs : [1.0000006 1.0000002 1.0000002]
それぞれの色空間の定義に則っているのが確認できます。
1×1畳み込み
NumpyやKerasの場合、チャンネルの軸が最後にあったのでそのままどんとテンソル積をとってあげれば大丈夫でした。しかし、PyTorchの場合はchannels_firstなので、そのまま積を取るというわけにはいかなくなります(einsumの関数を使えば書けるだろうけど自分はやりたくない)。
ここで畳み込みの計算定義(Conv2D)を思い出しましょう。自分が書いた記事からの図ですが、
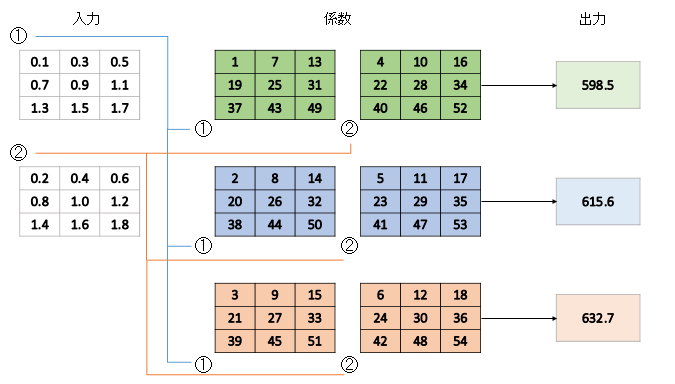
これは3×3カーネルの場合です。しかし、カーネルが1×1だったらどうでしょう? 行列単位で見ればドット積と変わらなくなりますよね。つまり、1×1畳み込みはテンソル積の計算関数として使えるということなのです。
PyTorchでの1×1畳み込みによるテンソル計算
全体のコードを貼ります。
import torch
import torch.nn.functional as F
import numpy as np
from PIL import Image
RGB2YCrCb = np.array([[0.299, 0.587, 0.114],
[0.5, -0.418688, -0.081312],
[-0.168736, -0.331264, 0.5]], np.float32)
YCrCb2RGB = np.array([[1, 1.402, 0],
[1, -0.714136, -0.344136],
[1, 0, 1.772]], np.float32)
def pytorch_version():
with Image.open("color_bar.png") as img:
rgb_array = np.asarray(img, np.float32) / 255.0
# PyTorchのためにNHWCをNCHWとする
rgb_array = np.expand_dims(rgb_array, axis=0)
rgb_array = np.transpose(rgb_array, [0,3,1,2])
rgb_tensor = torch.as_tensor(rgb_array)
print("RGB original")
print(rgb_tensor.size())
check_range(rgb_tensor)
print()
# 右から掛ける場合でも転置はいらない
weight_tensor = torch.as_tensor(RGB2YCrCb.reshape(3,3,1,1))
ycrcb_tensor = F.conv2d(rgb_tensor, weight_tensor)
print("Coverted to YCrCb")
print(ycrcb_tensor.shape)
check_range(ycrcb_tensor)
print()
weight_tensor = torch.as_tensor(YCrCb2RGB.reshape(3,3,1,1))
recon_tensor = F.conv2d(ycrcb_tensor, weight_tensor)
print("Reconstrunction RGB")
print(recon_tensor.shape)
check_range(recon_tensor)
def check_range(img_tensor):
img_array = img_tensor.numpy()
img_array = np.transpose(img_array, [0,2,3,1])
x =img_array.reshape(-1, img_array.shape[3])
mins = np.min(x, axis=0)
maxs = np.max(x, axis=0)
print("mins :", mins)
print("maxs :", maxs)
if __name__ == "__main__":
pytorch_version()
ポイントは「F.conv2d(rgb_tensor, weight_tensor)」の部分です。
引数の順番はnp.dotやK.dotと同じです。つまり、畳み込みのカーネル部分にかける側のテンソルを入れればよいということです。ただし、weight_tensorは4階テンソルにします。shapeの詳細は(出力チャンネル, 入力チャンネル, カーネルサイズ1, カーネルサイズ2)なので、今回の場合は「(3,3,1,1)」とするのが正しいです。
また、np.dotやK.dotと異なるのは、変換行列の転置が不要ということです。畳み込みの内部実装でやっているのでしょう。
結果は次のようになります。
RGB original
torch.Size([1, 3, 800, 1280])
mins : [0. 0. 0.]
maxs : [1. 1. 1.]
Coverted to YCrCb
torch.Size([1, 3, 800, 1280])
mins : [ 4.4705885e-04 -5.0000000e-01 -5.0000000e-01]
maxs : [1. 0.5 0.5]
Reconstrunction RGB
torch.Size([1, 3, 800, 1280])
mins : [-5.3644180e-07 -1.7881393e-07 -1.9312506e-07]
maxs : [1.0000006 1.0000002 1.0000002]
確かにうまくいきました。これは使えそうですね。
まとめ
Conv2Dは1×1カーネルにすれば普通のテンソル積の計算もできる。PyTorchの場合、チャンネルが一番外の軸ではないのでこの方法が有効。パフォーマンス面からはいちいち軸を入れ替えてmatmul取るよりこの方法が良いのでは? ということでした。多分変態実装言われそう
Shikoan's ML Blogの中の人が運営しているサークル「じゅ~しぃ~すくりぷと」の本のご案内
技術書コーナー
北海道の駅巡りコーナー

