ディープラーニング=最小二乗法のどこがダメなのか解説する

あるニュース記事で、ディープラーニング=最小二乗法で三次関数なんていう「伝説の画像」が出回っていたので、それに対して突っ込みつつ、非線形関数という立場からディープラーニングの本当の表現の豊かさを見ていきたいと思います。
目次
きっかけ
ある画像が出回っていた。日経新聞の解説らしい。
伝説の画像になるぞこれhttps://t.co/CpeWKrHseP pic.twitter.com/qfTUVt5j7A
— 猫じゃら美少女 (@tonets) 2019年2月19日
確かにこれは伝説の画像だ。今までディープラーニングの入門書を立ち読みしていても、ディープラーニング=最小二乗法で三次関数なんて解説は見たことがない。画期的な説明だ。
しかし、この画像、ディープラーニングを少しでもやったことある人から見ればかなり違和感を覚える解説だと思う。そこを突っ込み始めるとディープラーニング、あるいはニューラルネットワークのかなり本質的な部分に突っ込んでいくことになるのでそれを少しではあるが見ていきたい。
この著者の名誉のために捕捉しておくと、この解説は「ニューラルネットワーク=人間の脳」という根拠のない解説よりかは百倍も良い。ディープラーニングは関数の近似というアプローチは正しいが、ある大きな要素が抜け落ちているため「伝説の画像」となってしまったのだ。
ちなみにディープラーニングではほぼニューラルネットワークというモデルを使うため、ニューラルネットワーク≒ディープラーニングと考えても構わない。
活性化関数
ディープラーニングもとい、ニューラルネットワークには「活性化関数」という大きな要素がある。活性化関数とは一言で言えば、ニューラルネットワークの表現力を高めるための関数である。これにより非常に多種多様な表現を行うことが可能になっている。
活性化関数といってもいろいろあるが、代表的な2つ、ReLUとSigmoidをプロットしてみた。
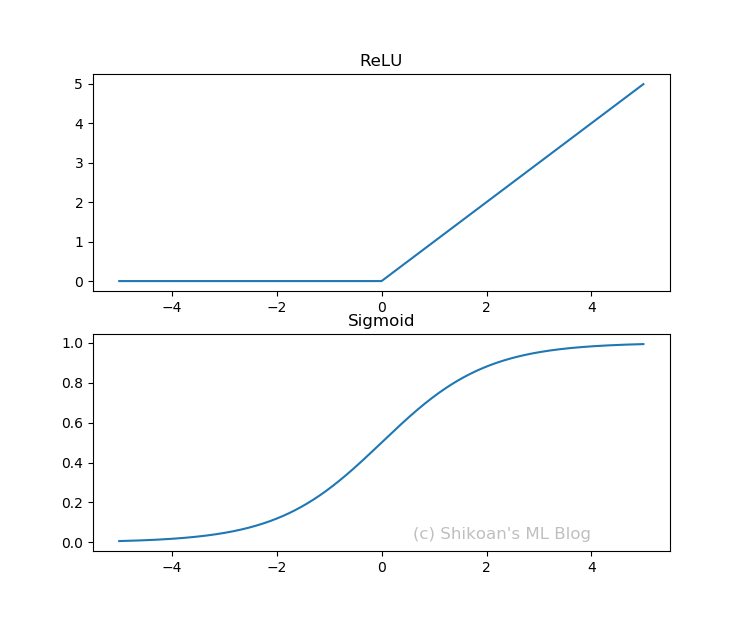
上がReLUで、下がSigmoidである。ReLUはRectified Linear Unitの略。このように曲がってたり、ぐんにゃりしたグラフなのが活性化関数の特徴である。ちなみにこんな風にぐんにゃりとか曲がってるとかを数学の言葉では非線形関数という。実は、この非線形関数によりディープラーニングは非常に豊かな表現力を確保しているのである。
ちなみにReLUとSigmoidを数式で書くと次のようになる。
$$ReLU(x)=\max(x,0) $$
$$Sigmoid(x)=\frac{1}{1+\exp(-x)} $$
線形な関数とは$f(x)=ax$のような関数であるが、線形関数のような簡単な式ではないのはわかるだろう。ReLUは2つの直線の合成のように見えるが、SigmoidもReLUも線形関数ではなく非線形関数だ。もし確かめてみたいのなら、「ReLU(-1)+ReLU(3)≠ReLU(-1+3)」であることを確かめてみればOKである(線形関数ならこれが成り立つ)。
非線形関数自体もそれはそれで表現力があるのだが、ニューラルネットワークでの強さはそれらの組み合わせにある。このような図を見たことがないだろうか。
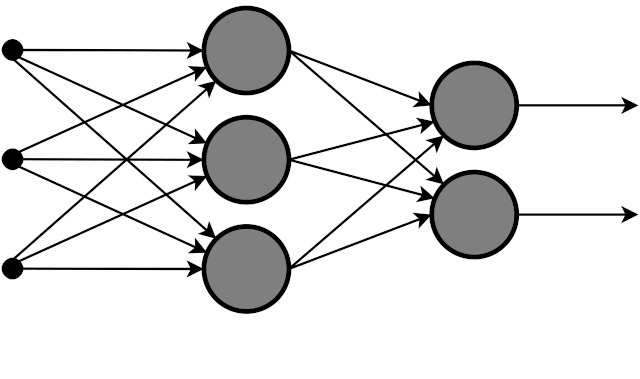
実はこれはニューラルネットワークの組み合わせを表現した図なのだ。各点(ニューロンという)では、入力に対して活性化関数を計算し、その次の層の入力にわたす。そして次の層でも活性化関数を計算し……と連続的に計算を行う。これがニューラルネットワークのやっていることだ。数式で表すと、活性化関数を$f(x)$とすると、
$$b_1f(a_1f(x_1)+a_2f(x_1)+\cdots+a_nf(x_n))+b_2f(\cdots)+\cdots $$
このように何層にも何層にも活性化関数を適用しているのがわかるだろうか。これがニューラルネットワークが多種多様な表現を獲得できる理由だ。
ポイント:ニューラルネットワーク(ディープラーニング)は非線形関数である活性化関数を何層にも何層にも組み合わせることで多種多様な強い表現力を獲得することが可能である
活性化関数を組み合わせると…
非線形関数の活性化関数を組み合わせるとどうなるのか確かめてみたい。ここでは次のようなプログラムを用意してみた。
import matplotlib.pyplot as plt
import numpy as np
def plot_relus(offset, coef):
x = np.arange(-10,10,0.01)
y = np.zeros(x.shape)
for off,c in zip(offset, coef):
y += c*np.maximum(x-off, 0)
return y
offset = np.random.uniform(-7,7,10)
coef = np.random.uniform(-0.2,0.5,10)
for i in range(len(offset)):
x = np.arange(-10,10,0.01)
y = plot_relus(offset[:i+1], coef[:i+1])
plt.clf()
plt.plot(x,y)
plt.show()
ReLUと切片と係数を変えて1個~10個まで合成してみる。複雑なカーブになっているのがわかるだろうか。
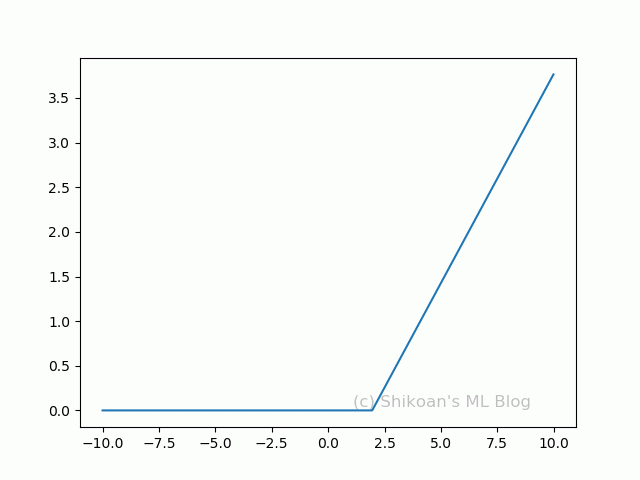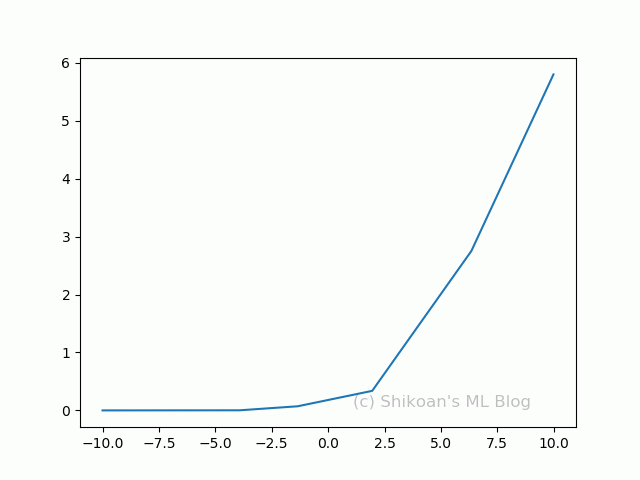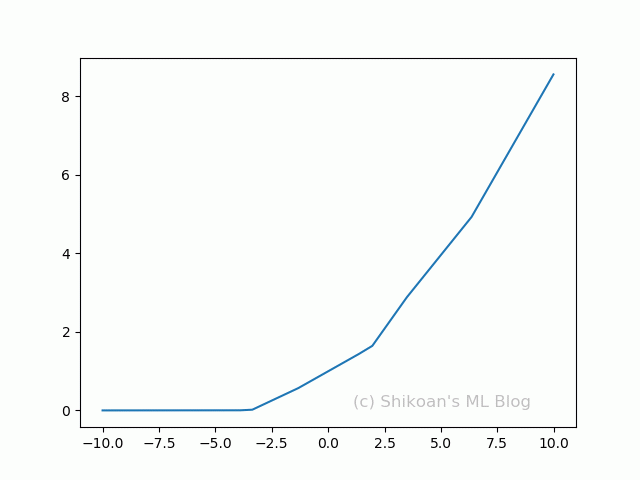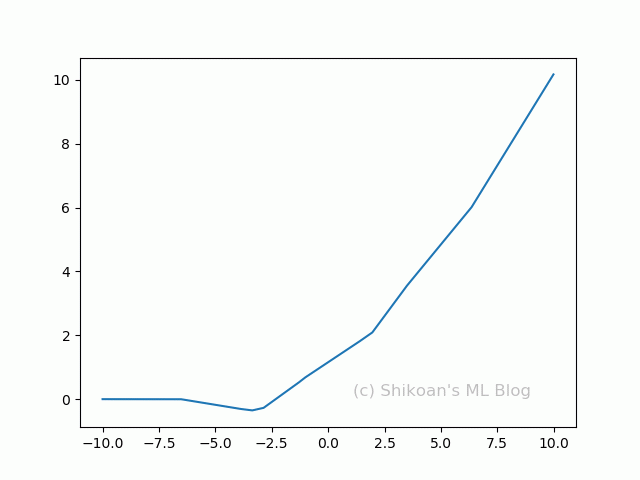
実際のディープラーニングでは、この組み合わせ(隠れ層)を1000個だろうが、横に10層だろうが当たり前のように使っていく。それだけ組み合わせればありとあらゆる表現ができるのも納得できるだろう。
豊かな表現の具体例
先程、ディープラーニングは関数の近似という説明をした。でも数学的には到底関数と考えづらいものまで関数と考えることができるのだ。

わかりやすいのは画像だろう。例えば、この画像をXとし、Xが猫なら1、Xが猫でないなら0という関数を考える。これが実際どういう数式なのか、紙で書き表すのは到底不可能だと思う。
ただし、ディープラーニングならできる。なぜなら、大量の非線形関数を何層にも、何重にも組み合わせているからである。あくまで紙に書き表せないぐらいの大量の関数を使っているというだけなのである。これがディープラーニングの「豊かな表現」であり、人間の目や耳に相当することをコンピューター上で行える根拠となっている。
ポイント:非線形関数の活性化関数を大量に組み合わせると、画像や音声、文章の内容だって関数で表現できる
最小二乗法だけではない
実は従来の統計的な最小二乗法(線形回帰)というのは、ディープラーニングでも表現できる。ただし、あくまで最小二乗法はディープラーニングの表現の一部でしかなく、それだけではない。
具体的には、最小化のターゲットである「損失関数」の選択の問題に帰着する。直感的には、「何で最適化したいの?」というターゲットである。これを変えることで、最小二乗法のような線形回帰から、確率の回帰を使った分類問題(統計的にはこれはロジスティック回帰と呼ばれる)、あるいは2つの系列(データ)を同じような分布にしていくような最適化も可能である。つまり損失関数の選択により、様々な表現することが可能である。もちろんこの損失関数は任意に定義することができる。ちなみに最小二乗法となる、損失関数はMean Squared Error(平均二乗誤差)と呼ばれる。
ポイント:最小二乗法(平均二乗誤差)はあくまで損失関数のひとつの選択。損失関数を変えればもっといろんな表現はできる。
実は三次関数の近似は従来の統計でもできる
この記事の書き方だと三次関数のような複雑な近似はディープラーニングでしかできないように思えるが、従来の線形回帰でも三次関数は近似できる。例えば、以下のような関数で表されるデータを最小二乗法で求めてみよう。
$$y=x^3-3x^2+5x-7 $$
import numpy as np
from sklearn.linear_model import LinearRegression
xvec = np.arange(-5,5,0.01)
X = np.c_[xvec**3, xvec**2, xvec, np.ones(xvec.shape)]
y = xvec**3 - 3*xvec**2 + 5*xvec - 7
ols = LinearRegression(fit_intercept=False).fit(X, y)
print(ols.coef_)
「ols.coef_」では最小二乗法の係数の推定値を表示できる。出力は以下の通り。
[ 1. -3. 5. -7.]
このように、三次関数でも最小二乗法で計算できた。ここでは一切ディープラーニングを使っていない。
ディープラーニングの強みとは、非線形関数を使ったモデリングにあり、三次関数のような簡単な場合だと従来の最小二乗法でも同じように表現できてしまうケースがある。
非線形関数を使ったモデリングの弱みと解決法
実は従来の統計でも非線形関数を使ったモデリングというのは考えられていた。ただし、計算上のコストが多かったりアルゴリズム上や計算資源上の問題があったため、知る人ぞ知るポジションでしかなかった。
実はディープラーニングでも同じ問題というのは直面したが、アルゴリズムの発展やGPUの活用、ディープラーニング専用のフレームワークといったブレイクスルーにより、そこの問題をあまり気にすることがなく、最小二乗法と同じような感覚で使うことが可能となっている。
アルゴリズムの発展:Back Propagation
アルゴリズムの発展とは、大きな功績はHinton先生らによるBack Propagation(誤差逆伝播法)だろう。ニューラルネットワークを最適化するには、多層の非線形関数に対する偏微分を計算しないといけない。ただしこれをそのまま(Xに微小な値を足して差分を取ると)計算するとえらいコストが大きいが、Back Propagationというアルゴリズムを使うと、ニューラルネットワークを逆方向にたどることで効率よく微分を計算することができる。簡単に言うと(偏)微分を高速に計算するためのテクニックだ。このBack Propagationは現在のディープラーニングでほぼ確実に使われている。
GPUの活用
GPUの活用とは、実はディープラーニングのやっていることは大量の行列やテンソル(行列の軸を3つ以上にしたもの)の計算である。GPUのようなグラフィックデバイスは、コンピューターグラフィックを行列計算のアプローチからやっている。例えば3Dゲームを考えてみればわかるだろう。コンピューターグラフィックとは、RGBAのような画素値をXY方向に展開し、さらに時間軸で変化させていくためやっていることはほぼ行列計算である。なのでコンピューターグラフィックに最適化しているGPUは行列計算に非常に強く、このような行列をCPUよりも高速に計算することができる。もしこのへんに興味があるのなら、NVIDIAが出している動画が非常にわかりやすいのでぜひ見てほしい。直感的なデモだがかなり本質的な説明である。
ディープラーニングのフレームワーク
ディープラーニングの専用のフレームワークも大きく貢献している。例えば、TensorFlowやChainer, PyTorch, Keras, MXNet, Caffeといった言葉を聞いたことのある方もいると思う。これらはディープラーニングの専用のフレームワークだ。なぜこれらが有用かというと、実際にGPUで計算をしようとすると、GPGPU(GPUを使った汎用計算)の知識、具体的にはCUDAの知識が必要になって非常に低レベルの部分からプログラミングしなければならない。これらをいい感じにやってくれて、使う側はニューラルネットワークを組む部分だけを定義すればいいのが、ディープラーニングのフレームワークである。使っている側としてはほぼ最小二乗法に毛が生えた程度の認識で使うことができる。
またこれらのフレームワークの多くは自動微分という機能を持っていて、先程のBack Propagationを自分で定義することなく、フレームワーク側で勝手に計算してくれるというとてもありがたい機能がある。微分の定義をいちいち意識しなくていいのはとても楽である。
まとめ
以上、アルゴリズム面、デバイス面、フレームワーク面の少なくとも3点の貢献により、ディープラーニングは非線形関数の組み合わせという従来の統計でもなかなか難しかった問題を乗り越え、今まさに普及期に入っているといえるだろう。
Shikoan's ML Blogの中の人が運営しているサークル「じゅ~しぃ~すくりぷと」の本のご案内
技術書コーナー
北海道の駅巡りコーナー

