TensorFlowの関数で画像にモザイクを書ける方法

---

TensorFlow2.0の関数を使い、画像にモザイクをかける方法を紹介します。OpenCVやPILでの書き方はいろいろありますが、TensorFlowでどう書くかはまず出てきませんでした。GPUやTPUでのブーストも使えます。

モザイク付与のアルゴリズム

いろいろあるとは思いますが、自分が使っているのは次の方法です。

• Nearest Negihbor法で1/Nの解像度にダウンサンプリング（Nは元の画像の解像度にあわせて適当に調整）
• 適当なサイズのカーネルのガウシアンぼかしをかける
• Nearest Neighbor法でN倍にアップサンプリング

環境：TensorFlow2.0.0

実装

この画像を「ramen.jpg」とし、モザイクをかけてみます。

import tensorflow as tf
import matplotlib.pyplot as plt
import numpy as np

def load_image():
    # ファイルを読み込みJPEGをデコード (このオペレーションはTPUでは不可能なので注意)
    return tf.io.decode_jpeg(tf.io.read_file("ramen.jpg"))

def add_mosaic(inputs):
    # 0-1スケールに変換（ここからTPUでも実行可能）
    x = tf.image.convert_image_dtype(inputs, tf.float32)
    # 4階テンソルで考える
    x = tf.expand_dims(x, axis=0)

    # ガウシアンぼかしのカーネル
    kernel = np.array([
        [1, 4, 6, 4, 1],
        [4, 16, 24, 16, 4],
        [6, 24, 36, 24, 6],
        [4, 16, 24, 16, 4],
        [1, 4, 6, 4, 1]], np.float32) / 256.0
    gaussian_kernel = tf.constant(np.broadcast_to(kernel.reshape(5, 5, 1, 1), (5, 5, 3, 1)))

    # Nearest Neighborのダウンサンプリング
    x = tf.image.resize(x, size=(x.shape[1] // 16, x.shape[2] // 16),
                        method=tf.image.ResizeMethod.NEAREST_NEIGHBOR)
    # ガウシアンぼかし
    x = tf.nn.depthwise_conv2d(x, gaussian_kernel, strides=[1, 1, 1, 1], padding="SAME")
    # Nearest Neighborのアップサンプリング
    x = tf.image.resize(x, size=(x.shape[1] * 16, x.shape[2] * 16),
                        method=tf.image.ResizeMethod.NEAREST_NEIGHBOR)
    return x

if __name__ == "__main__":
    x = load_image()
    mosaic = add_mosaic(x)
    plt.imshow(mosaic.numpy()[0])
    plt.show()

注意：このコードをTPUで実行したところ、リサイズ部分の挙動がおかしくて正しい挙動になりませんでした。ご注意ください（TF2.0）。

結果は以下の通り

いい感じにモザイクかかっていますね。周囲が黒くなっているのはPaddingの影響です。もしここが気になるのなら、tf.padのモードをREFLECTにして、事前にReflect paddingするとよいでしょう。

Depthwise Conv vs Conv2D

このコード、ガウシアンぼかしの部分にDepthwise Convを使っているのが特徴です。以前の記事では（PyTorchですが）、チャンネルごとにConv2DをかけてConcatするという方法を取りました。チャンネルごとにConv2DをかけてConcatするというのと、Depthwise Convは実は同じことです（これに気づいてうおおおおってなりました）。

確認してみましょう。Depthwise Convでガウシアンぼかしをかけた例と、チャンネル単位にConv2Dでガウシアンぼかしをかけた例で誤差を取ります。比較例として、ガウシアンぼかしをかける前後での誤差も同様に取ります。誤差はL1ロスで計測します。

def depthwise_conv_check():
    inputs = load_image()
    x = tf.image.convert_image_dtype(inputs, tf.float32)
    base_img = tf.expand_dims(x, axis=0)

    # ガウシアンぼかしのカーネル（DepthwiseかConv2Dかでカーネルのshapeが違うので注意）
    kernel = np.array([
        [1, 4, 6, 4, 1],
        [4, 16, 24, 16, 4],
        [6, 24, 36, 24, 6],
        [4, 16, 24, 16, 4],
        [1, 4, 6, 4, 1]], np.float32) / 256.0
    depthwise_kernel = tf.constant(np.broadcast_to(kernel.reshape(5, 5, 1, 1), (5, 5, 3, 1)))

    # ガウシアンぼかし
    depthwise_blur = tf.nn.depthwise_conv2d(base_img, depthwise_kernel, strides=[1, 1, 1, 1], padding="SAME")

    # Conv2dによる計算
    conv_kernel = tf.constant(kernel.reshape(5, 5, 1, 1))
    multichannel = [tf.nn.conv2d(base_img[:,:,:, i:i + 1], conv_kernel, strides=[1, 1, 1, 1],
                    padding="SAME") for i in range(3)]
    conv_blur = tf.concat(multichannel, axis=-1)

    # depthwiseとconv2dの差分
    method_diff = tf.reduce_mean(tf.abs(depthwise_blur - conv_blur))
    print(method_diff.numpy())

    # オリジナルとガウシアンぼかしの差分（比較用）
    blur_diff = tf.reduce_mean(tf.abs(depthwise_blur - base_img))
    print(blur_diff.numpy())

結果は次のようになりました。

• Depthwise ConvとConv2Dによるガウシアンぼかし同士の誤差は、8e-9と十分に小さい
• 元画像とガウシアンぼかしとの誤差（差分）は、0.01とそこそこ大きい

Depthwise ConvもConv2Dもガウシアンぼかしを取れる→つまり、Depthwise Convでいいということになります。

8.543839e-09
0.014340522

なぜDepthwise Convなのか

以前に自分が書いた記事を思い出しました

具体例で覚える畳み込み計算（Conv2D、DepthwiseConv2D、SeparableConv2D、Conv2DTranspose）
https://qiita.com/koshian2/items/885aba771190267a3a1c

これを見るとなんとなくわかると思います。

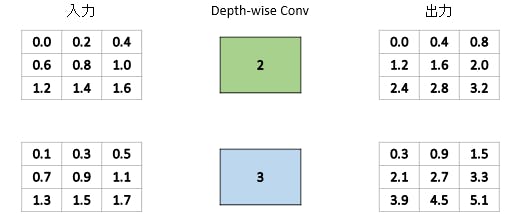
Depthwise ConvはConv2Dと異なり、畳込みを取ったあとレイヤー同士で和を計算するということをしない、つまりチャンネル単位で独立に計算をしているのです。

これはガウシアンぼかしだけではなく、OpenCVなどで定義されているディープラーニング以前の画像処理での畳込みとは、ほぼDepthwise Convであるということを示しているにほかなりません。

まとめ

• TensorFlowでもモザイクはかけられるよ
• OpenCVなどで定義されているディープラーニング以前の画像処理での畳込みとは、ほぼDepthwise Conv

特に下は面白い知見ではないでしょうか

---

---

Shikoan's ML Blogの中の人が運営しているサークル「じゅ～しぃ～すくりぷと」の本のご案内

---