Kernel-PCAのexplained_variance_ratioを求める方法

---

scikit-learnのPCA（主成分分析）にはexplained_variance_ratio_という、次元を削減したことでどの程度分散（データを説明できる度合い）が落ちたのかを簡単に確認できる値があります。Kernel-PCAではカーネルトリックにより、特徴量の空間が変わってしまうので、explained_variance_ratio_というパラメーターは存在しません。ただこの値はハイパーパラメータのチューニング用にとても便利なので、説明分散比を擬似的に求める方法を書きます。

主成分分析（PCA）の説明分散比

主成分分析の説明分散比はPCA.explained_variance_ratio_で簡単に求めることができますが、どのような計算をしているか確認するためにNumpyで書いてみます。Irisデータセットを使います。

import numpy as np
from sklearn.datasets import load_iris
from sklearn.decomposition import PCA, KernelPCA

iris = load_iris()
X, y = iris["data"], iris["target"]

## 主成分分析
pca = PCA(n_components=2)
# 主成分分析で変換
X_pca = pca.fit_transform(X)
# 分散比の計算
manual_var = np.sum(np.var(X_pca, axis=0) / np.sum(np.var(X, axis=0)))
print("Manual explained var ratio :", manual_var)
print("Built-in explianed var ratio :", np.sum(pca.explained_variance_ratio_)) #この2つが一緒になっていることを確認する

主成分分析で2次元に削減します。分散比を手動で計算する場合は、np.sum(np.var(X_pca, axis=0) / np.sum(np.var(X, axis=0)))で計算できます。次元単位で分散比を求めたい場合は外側のsumを外してください。これはsklearnのPCA組み込みのexplained_variance_ratio_と一致します。

Manual explained var ratio : 0.9776317750248044
Built-in explianed var ratio : 0.9776317750248034

ね？一致してますよね。これがexplained_variance_ratio_の中身です。

ところが、このexplained_variance_ratioはPCAだけだとうまくいくのですが、Kernel-PCAで非線形のカーネルを使う場合（例：rbfカーネル）は特徴量の空間が変わってしまうので、良い評価尺度とはいえません。そこで、PCAとKernel-PCA両方で使える分散比の評価尺度を定義します。

sklearn.metrics.explained_variance_scoreを使うと、y_trueとy_predを代入することで説明分散比を計算してくれます。ここで、y_predにはPCA（またはKernelPCA）で変換した行列を逆変換したものを代入します。sklearnではinverse_transformという関数で逆変換ができます（これはPCA,KernelPCA両方あります）。主成分分析の変換は非可逆なので、transformで一度分散が落ちてしまうと、inverse_transformで元の次元に戻そうが分散が落ちた状態で返ってくるというわけです。これを説明分散比の代用とします。

from sklearn.metrics import explained_variance_score

# kernel-PCAだと特徴量の空間が変わってしまうので、逆変換したもので分散を比較する
# （PCA.explained_variance_ratio_とは異なる値を返す）
var_score = explained_variance_score(X, pca.inverse_transform(X_pca))
print("Explained variance score : ", var_score)
print()

Explained variance score : 0.9326484048695863

ただし、これはPCA.explained_variance_ratio_とは異なります。なぜなら、explained_variance_ratio_は逆変換したもので比較していないからです。変換→逆変換と2回分変換しているので、主成分分析の場合おそらくexplained_variance_scoreのほうがexplained_variance_ratio_よりも低くなるはずです。explained_variance_scoreの意義とは、カーネルトリックを使った場合でも主成分分析と同一の尺度で説明分散比を求めることができるということにあります。

ちなみに主成分分析で変換した結果をプロットすると次のようになります。

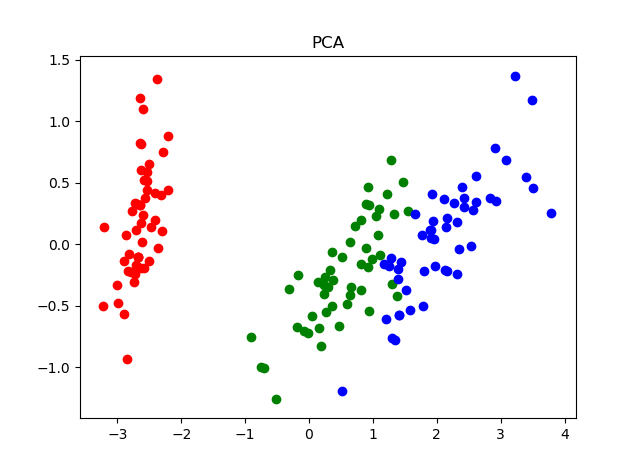
Irisの場合は決定境界は線形関数で表さそうなので、主成分分析がとてもよく機能している例です。

Kernel-PCAの説明分散比

同様にIrisをRBFカーネルで2次元にしてみます。イメージ的にはサポートベクターマシンのRBFカーネルとほぼ同じです。gammaというハイパーパラメータがありますが、説明分散比が高くなるようにチューニングします。

## Kernel PCA
kpca = KernelPCA(n_components=2, gamma=0.1, kernel="rbf", fit_inverse_transform=True)
# Kernel PCAで変換
X_kpca = kpca.fit_transform(X)
# 分散比（kpca.explained_variance_ratio_は存在しないことに注意）
print("Explained var ratio :", np.sum(np.var(X_kpca, axis=0) / np.sum(np.var(X, axis=0)))) #不適切
print("Explained var score :", explained_variance_score(X, kpca.inverse_transform(X_kpca)))

上が主成分分析のexplained_variance_ratio_と同じ方法で計算した結果、下がexplained_variance_scoreで計算した結果です。

Explained var ratio : 0.08406470350792002
Explained var score : 0.7846466165602104

明らかに値が変わっています。上の値から見ると92%も分散が落ちているように見えますが、これは特徴量の空間が変わったためで、X_kpcaとXを同一の分散で比較できなくなったためです。92%も分散が落ちていないのはプロットしてみればわかります。

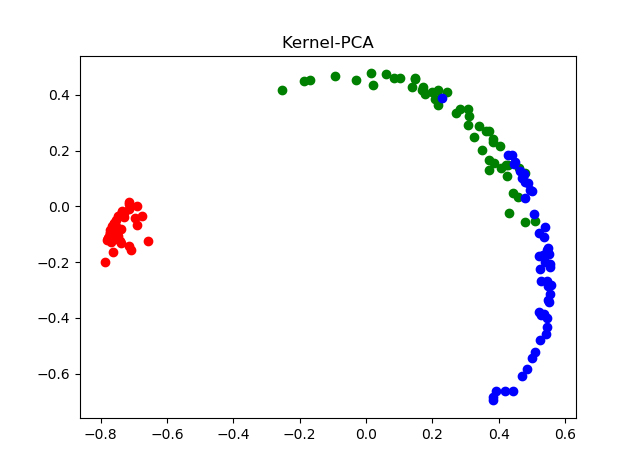
円形状になってしまったのは、ガウスカーネルの性質によるものです。主成分分析で92%も分散が落ちてしまったらほぼランダムに近い状態になるはずですが、円形状ではあるもののクラス（この場合はアヤメの品種）単位で似たような場所にあることが確認できます。なので、主成分分析と同じイメージで92%も分散が落ちたとは言えません。

つまり、KernelPCAの場合は下のexplained_variance_scoreの78%を見ましょう。PCAのではexplained_variance_scoreは93%でしたので、Irisで2次元に落として可視化する場合はKernelPCAよりもPCAのほうが適切ということがわかります。Irisの各パラメーターがそれぞれ線形寄りの決定境界を持っているためそれはそうですね。

Kernel-PCAの次元単位の分散比

KernelPCAにおいて次元単位で分散比を見たい場合（つまりどの軸がより多く分散を説明できているか）があると思います。その場合はexplained_variance_ratioのアプローチを使ってOKです。

## KernelPCAの次元単位の分散比（これはX_kpcaの中で分散比を計算すればよい）
kpca_var_vec = np.var(X_kpca, axis=0) / np.sum(np.var(X_kpca, axis=0))
print(kpca_var_vec)

なぜOKかというと、分子も分母も同一のX_kpcaという同一の空間を用いているためです。X_kpcaとXのように異なる空間で分散を比較してはダメですよというだけです。

[0.78933126 0.21066874]

プロット見ればわかるように第1軸（横軸）のほうがより多く分散を説明できていますね。

まとめ

KernelPCAに限らずとも、「次元削減アルゴリズムでどれがいい？」となったときにexplained_variance_scoreを共通の尺度として比較するという方法は有効だと思われます。

---

---

Shikoan's ML Blogの中の人が運営しているサークル「じゅ～しぃ～すくりぷと」の本のご案内

---