NumPy+waveでファミコン風の音色を自作する
NumPyを使って、矩形波、25%/12.5%パルス波、三角波、ノイズなどファミコン音源で使われているような音色を実装してみました。周波数のコントロールと併用すれば、NumPyはシンセサイザーとしても活用できます。
目次
基本の正弦波
まず基本。正弦波はファミコンの音楽で使うことはあまりないですが、関数化しやすいので最初に導入するのが便利です。サンプリング時は、次のような関数を作ることになります。
def some_wave_function(freq, t):
# freq: 周波数(数値)
# t: 時刻(ベクトル)
return 何らかの波形
freqは周波数を示します。これで音階をコントロールします。
tは時刻(秒ベース)のベクトルを表します。1秒間音を鳴らすのなら、0~1がtとして与えられます。tの長さはサンプリングレートによります。サンプリングレートが44100Hzで1秒間音を鳴らすのなら、tの長さは44100になります。
正弦波の場合、次の式になります。簡単な式で表されるのは正弦波ぐらいなのでコードでかければいいです。
$$y=sin(2pi ft)$$
コードで書くと次のようになります。
import numpy as np
import matplotlib.pyplot as plt
def sine(freq, t):
return np.sin(2*np.pi*freq*t)
出力のスケールは-1~1になります。WAVEファイルに変換するときは量子化が必要で、ビット数に応じた定数をかけて整数とするプロセスが別途追加します。
実際に1Hzの正弦波を5秒発生させてグラフにプロットしてみましょう。1Hzなので1周期は1秒になります。
x = np.linspace(0, 5, 44100*5+1)
y = sine(1, x)
plt.plot(x, y)
plt.show()
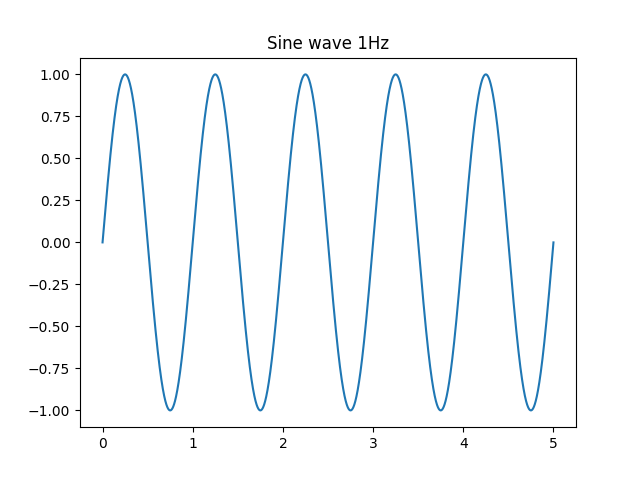
横軸の単位は秒です。周期が1秒(=1Hz)の波が生成されました。周波数を2倍(2Hz)にしてみましょう。「sine(2, x)」とするだけです。
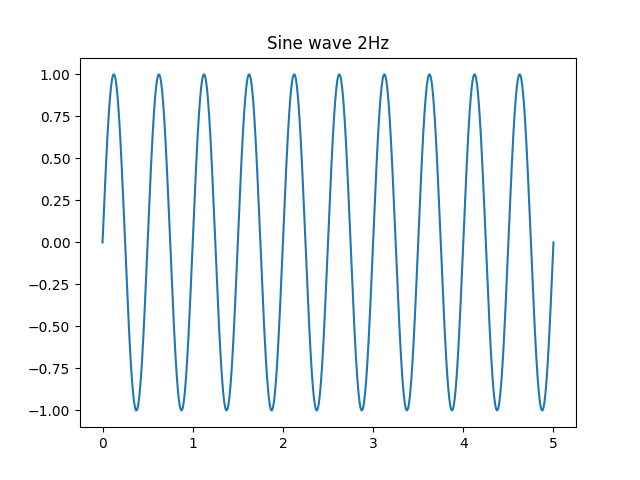
波がより密になりました。周波数を上げるほど高い音になります。ただ、1Hzも2Hzも人間には聞こえない音です。音の基本となっている440Hzのラの音をWAVEファイルとして生成してみます。
def ra_synthesis():
sampling_rate = 44100 # サンプリングレートは44100Hz
x = np.linspace(0, 5, sampling_rate*5+1)
y = sine(440, x) # 440Hz
# 量子化
y = (y*32767).astype(np.int16)
with wave.Wave_write("ra_sine.wav") as fp:
fp.setframerate(sampling_rate)
fp.setnchannels(1) # モノラル
fp.setsampwidth(2) # 16ビット(バイト数を入力する)
fp.writeframes(y.tobytes()) # バイナリ化
WAVEファイルの生成にはPythonの組み込みモジュールであるwaveを使用しています。まずは実際に鳴らしてみましょう(ブログにアップロード時にMP3に変換しています)。
sine関数の出力は浮動小数点数ですが、実際にWAVEファイルとして保存するには符号付き整数型である必要があります。どの整数型で保存するかは量子化ビット数によります。量子化とは、整数のデータ型に収まるようにスケーリングして、小数→整数と変換する処理です。NumPyではデータ型の最大値などをかけて、astypeで整数型へキャストすることでできます。
よく使うのは量子化ビット数は16です。量子化ビット数はサンプリングレートと同様に音質を決める、いわばハイパーパラメータですが、音楽CDではこの例のようにサンプリングレートが44.1kHz、量子化が16ビットとしています(参考)。16ビットだとnp.int16で即いけるのでPythonの処理的に都合がいいという事情もあります。
参考:http://nalab.mind.meiji.ac.jp/~mk/lecture/fourier-2018/python-sound/node7.html
矩形波
矩形波はファミコンの音楽でメロディ等によく使われる音色です。
このケースでは1周期のうちに山が50%、谷が50%の矩形波ですね。後に出てくる「25%パルス波」や「12.5%パルス波」も矩形波の一部です。ただこの記事では上の動画にならい、50%の矩形波を特に矩形波と呼ぶことにします。
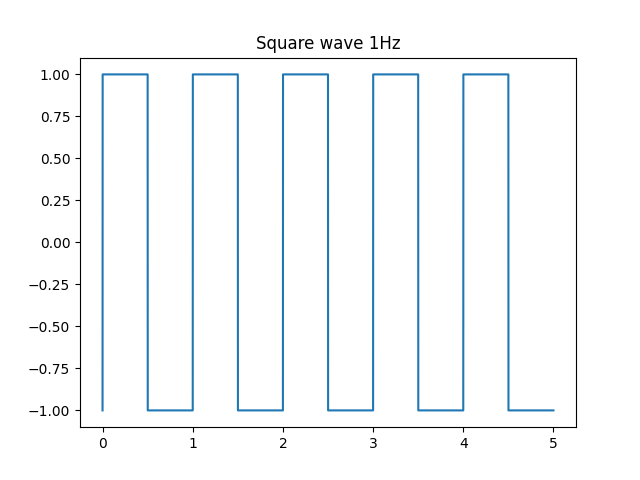
波形をグラフで書くとこんな感じですね。正弦波の合成で書くと面倒そうですが、単に山と谷なので、剰余と切り上げ(切り捨て)を活用すればNumPy関数で実装できそうです。
# 矩形波
def square(freq, t):
# [0-pi] -> 1, [pi-2pi] -> -1
return (np.ceil(t * freq * 2) % 2) * 2 - 1
正弦波と同様に440HzのラをWAVEファイルでサンプリングしてみましょう。コードは正弦波の場合と同様です。(正弦波と比べてうるさいので音量に注意してください)
25%パルス波
先程の矩形波を山を25%、谷を75%に変えたものです。矩形波の一部として扱われることもあります。
波形はこんな感じです。
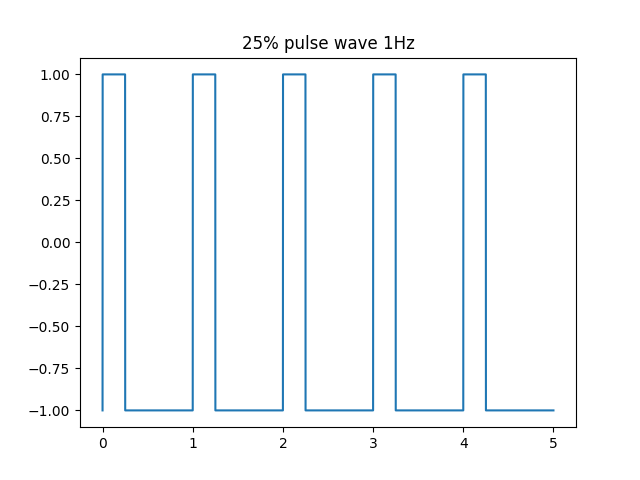
NumPyでの実装時は矩形波と同様、剰余を活用するとうまくいきそうです。剰余計算と切り上げで「0, 1, 2, 3, 0, 1, 2, 3…」とループするようにして、これが0の部分のみ1とするという計算です。
自分の実装では、これに山の部分が周期のはじめにくるように位相を調整しています。「t * freq * 4 – 1」の-1です。np.ceilのカッコ内で×4するのがポイントで、これが矩形波と同様に×2だと、オクターブ下がった音が出力されます。
# 25%パルス波
def pulse_quarter(freq, t):
return (np.ceil(t * freq * 4 - 1) % 4 == 0) * 2 - 1
実際に慣らしてみると次のとおりです。矩形波よりも歪みがかかった音になりますね。
12.5%パルス波
25%パルス波の山を12.5%にしたものです。山の領域が小さくなり、より歪みがかった音が出ることが予想されます。実装上は25%パルス波の数値だけ変えればいいです。
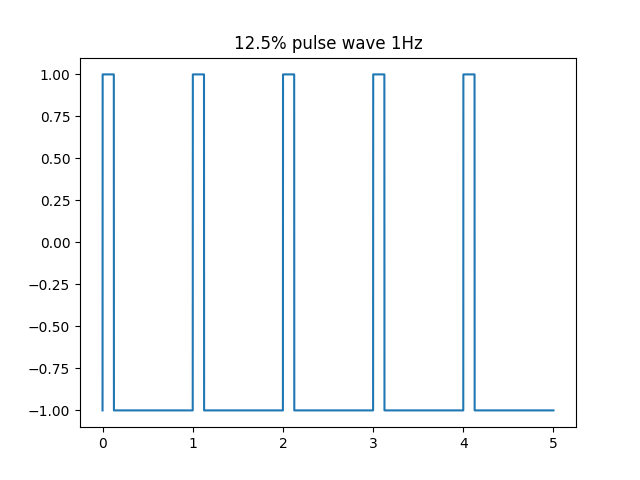
# 12.5%パルス波
def pulse_eighth(freq, t):
return (np.ceil(t * freq * 8 - 1) % 8 == 0) * 2 - 1
三角波
三角波はベースとして用いられることが多い音色です。波形は正弦波に似ていますがもっとカクカクした波形です。
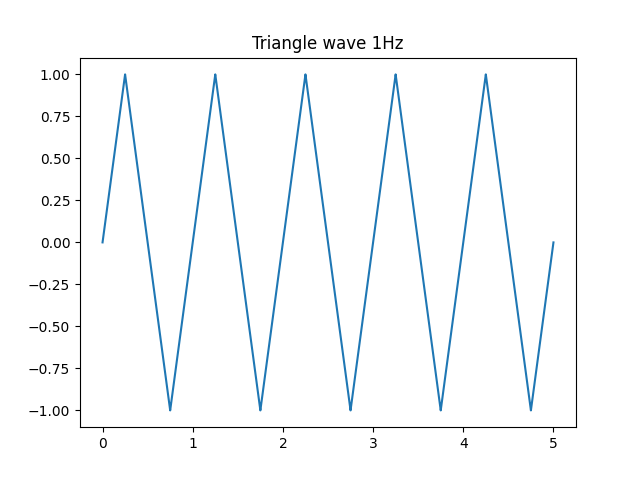
少し考えるのが難しかったのですが、剰余と絶対値を組み合わせれば一本の式で表せました。
# 三角波
def triangle(freq, t):
return np.abs((2*t*freq-1/2)%2 - 1) * 2 -1
鳴らしてみましょう。
ノイズ
ノイズは効果音やパーカッションに使われます。
ノイズというと、正直「np.random.uniform」などでやればいいだけなんですが、それだと高性能なノイズで、あんまりファミコンっぽくありません。np.random.uniformだけでサンプリングしたのがこちら。
def noise_synthesis():
sampling_rate = 44100
# 高性能なノイズなのであんまりファミコンっぽくない
y = np.random.uniform(-1, 1, size=(sampling_rate*5+1,))
y = (y*32767).astype(np.int16)
with wave.Wave_write("random_noise.wav") as fp:
fp.setframerate(sampling_rate)
fp.setnchannels(1)
fp.setsampwidth(2)
fp.writeframes(y.tobytes())
ファミコンっぽくチープなノイズをできる限り目指してみます。ここからは自分がそれっぽく目指して実装したものなので、ファミコンの音源の再現を保証するものではありません。
こちらの動画の波形を見ていると、時間軸のサンプリングレートを下げてサンプリングするとそれっぽくなっているように見えます。サンプリングレート(44.1kHz)通りにサンプリングせず、もっと小さなレートで乱数生成して、画像でいうところのNearest Neighbor法による拡大を1次元で行い、サンプリングレートに戻す方向で実装してみます。これはNumPy関数で頑張ればできます。
ファミコンのノイズは周波数をある程度コントロールできるので、ノイズのサンプリングレートを引数の周波数と紐付けて乱数を発生させます。
def noise(freq, t):
duration = t[-1]-t[0]
coarse_x = np.linspace(t[0], t[-1], int(freq*20*duration)+1) # ここの倍率は要検討
coarse_noise = np.random.uniform(-1, 1, size=coarse_x.shape[0])
# 一次元のNearest Neighbor法
tile_n = int(np.ceil(t.shape[0]/coarse_x.shape[0]))
interpolate_noise = np.stack([coarse_noise for i in range(tile_n)], axis=-1)
return interpolate_noise.flatten()[:t.shape[0]]
「coarse_x」のfreq×durationにつく倍率が難しいです。ノイズのサンプリングレートを決めるためのパラメーターです。同じ入力周波数でも、この値を低くするとゴォーという低い音になり、高くするとnp.random.uniformに近いノイズになります。ファミコン音源の仕様を解析したサイトによると、
ノイズの周波数は、ファミコンのCPUのクロック周波数(1789772.5)を、除数で割った値である。
周波数 = 1789772.5 ÷ 除数
とあり、除数は4~4068のおおよその2のべき乗となっていました。4068を代入すると周波数は約440Hzとなるので、一番低い音でもこのぐらいでサンプリングすればいいのかなと解釈できます。人間の可聴域が下が20Hzぐらいなので、freq×durationに掛ける値が20ぐらいだとほぼほぼこの仕様に一致するかなと思われます。かなり自分の勝手な解釈なので、もっといい方法があると思います。
入力周波数が1Hzでの波形はこちら(どう見ても1Hzじゃないですねみたいなツッコミはさておき)。
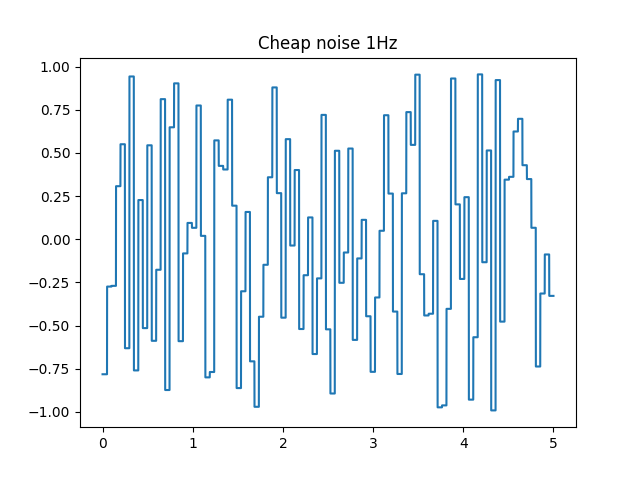
def noise_synthesis():
sampling_rate = 44100 # サンプリングレートは44100Hz
x = np.linspace(0, 6, sampling_rate*6+1)
y = np.zeros_like(x)
y[:sampling_rate*2] = noise(110, x[:sampling_rate*2])
y[sampling_rate*2:sampling_rate*4] = noise(220, x[sampling_rate*2:sampling_rate*4])
y[sampling_rate*4:] = noise(440, x[sampling_rate*4:])
# 量子化
y = (y*32767).astype(np.int16)
with wave.Wave_write("cheap_noise.wav") as fp:
fp.setframerate(sampling_rate)
fp.setnchannels(1) # モノラル
fp.setsampwidth(2) # 16ビット(バイト数を入力する)
fp.writeframes(y.tobytes()) # バイナリ化
入力周波数を110Hz,220Hz、440Hzとしてサンプリングしてみます。
かなりファミコンっぽくなりました。砂嵐の効果音でこんなの聞いたことがあるのではないでしょうか。
応用例
ファイナルファンタジーのプレリュードを、ここで実装したいろいろな音源を使って鳴らしてみました。音階から周波数は、
# 音階→周波数
def note_to_freq(notestr):
key, octave = notestr[:-1], notestr[-1]
keys = ["C", "C#", "D", "D#", "E", "F", "F#", "G", "G#", "A", "A#", "B"]
# 周波数起点はA(ラ)からなのに、オクターブはC(ド)からなので周期を調整する
return 27.5 * 2 ** (int(octave) + (keys.index(key)-9)/12)
のように計算します。notestrには「A4(中央ラ)」、「C4(ト音記号の下のド)」、「C#4(その半音上)」のように与えます。周波数と音階の関係は十二平均律を使っています。A4が440Hzなので、その4オクターブ下のA0は27.5Hzで、あとは指数関数という実装です。
NumPyから任意のWAVEファイルを吐かせれば、ファミコン音源のようにシンセサイザーとしても活用できます。
Shikoan's ML Blogの中の人が運営しているサークル「じゅ~しぃ~すくりぷと」の本のご案内
技術書コーナー
北海道の駅巡りコーナー

