TensorFlow/Kerasでの分散共分散行列・相関行列、テンソル主成分分析の実装

TensorFlowでは分散共分散行列や主成分分析用の関数が用意されていません。訓練を一切せずにTensorFlowとKeras関数だけを使って、分散共分散行列、相関行列、主成分分析を実装します。最終的にはカテゴリー別のテンソル主成分分析を作れるようにします。
何らかの論文でこれらのテクニックを使うことがあるかもしれません。
目次
これまでのまとめ
今回の内容はこれまでの内容のまとめです。TensorFlowでのグラム行列の導出や、グラム行列の期待値と分散共分散行列・相関行列の関係を理解した上で進めます。
- TensorFlow/Kerasでグラム行列(テンソル)を計算する方法
https://blog.shikoan.com/tensorflow-gram-matrix/ - 統計学や機械学習で使われる分散共分散行列、相関行列とグラム行列の関係
https://blog.shikoan.com/cov-corr-gram-matrix/
ざっくりおさらいすると次の通りです。
- TensorFlowでグラム行列をする際は、”’tf.matmul(X, X, transpose_a=True)”’で求められる。これはテンソルに対しても同じコマンドでいける
- データを平均で引いてグラム行列の期待値を取ると分散共分散行列になる。平均で引いて標準偏差で割る標準化をしてグラム行列の期待値を取ると相関行列になる。相関行列は分散共分散行列の特別な場合。
NumpyとTensorFlowにある関数のまとめ
実際NumpyとTensorFlowでどれぐらい関数の実装度合いが違うでしょうか。今回関係する関数を見てみます。
- 内積:Numpy=np.dot, np.matmulなど TF=tf.matmulなど
さすがにこれぐらいはある - 転置:Numpy=.T, np.swapaxes, TF=tf.transpose
さすがにこれもある。tf.transposeは引数のpermで並び順、swapaxesと同様のことをできる - 平均、標準偏差:Numpy=np.mean, np.std、TF=tf.reduce_mean, tf.nn.moments, K.mean, K.std
TensorFlowで標準偏差単体の関数はないらしい。ちなみにtf.nn.momentsという関数を使うと平均、分散を同時に計算できる。Kerasのバックエンド関数なら単体で可能。 - 分散共分散行列:Numpy=np.cov, TF=なし
ここらへんからTensorFlowの関数がない - 相関行列:Numpy=np.corrcoef、TF=なし
相関行列も自分で書かないとダメ - 固有値分解:Numpy=np.linalg.eig, np.linalg.eigh、TF=np.linalg.eigh
固有値分解はTFでは対称行列という条件付きでできる。主成分分析は分散共分散行列の固有値分解をするので一応計算可能(分散共分散行列は必ず対称行列なので)。出てくる結果はnp.linalg.eighと基本的に同じ。 - 特異値分解:Numpy=np.linalg.svd, TF=tf.linalg.svd
こちらは任意の行列でできる。TensorFlowで主成分分析したいときはこっちのほうが良いかもしれない。np.linalg.svdとnp.linalg.eigとtf.linalg.svdはどれも固有ベクトルと固有値を求められるが、固有ベクトルの符号が変わることがあるので注意(意味的には同じ軸を表しているので特にそれが気にならなければこっちでOK)。 - 主成分分析:NumpyもTFもなし
さすがに低レベルのAPIだとできない。ただしCPUではSklearnで一発でできる
ここらへんをまとめると前回、前々回でやったグラム行列からの導出というのがなかなか有用であるのが理解できるでしょうか。
TensorFlowでの分散共分散行列、相関行列の導出(行列版)
はじめに行列(ランク2テンソル)という条件付きで導出してみます。
TensorFlowで分散共分散行列
分散共分散行列は系列平均で引いてグラム行列の期待値を求めればよいのでした。Irisデータセットを使います。
from sklearn.datasets import load_iris
import keras.backend as K
import tensorflow as tf
import numpy as np
def tf_cov(input_tensor):
mean = tf.reduce_mean(input_tensor, axis=0, keepdims=True)
mean_adjust = input_tensor - mean
n_sample = tf.cast(tf.shape(input_tensor)[0] - 1, tf.float32) #不偏分散(N-1)で計算
gram_matrix = tf.matmul(mean_adjust, mean_adjust, transpose_a=True)
return gram_matrix / n_sample
if __name__ == "__main__":
iris_X, iris_y = load_iris(return_X_y=True)
iris_X_tensor = K.variable(iris_X)
cov_tensor = tf_cov(iris_X_tensor)
print("TensorFlow")
print(K.eval(cov_tensor))
print()
print("Numpy")
print(np.cov(iris_X, rowvar=False))
Numpyのnp.covがデフォルトで不偏分散で計算するので、今回はN-1に合わせました。サンプル数はTensorにする前にもっと簡単に取得できるので、そのときに0割り対策のassertをかけてあげればいいですね。
TensorFlow
[[ 0.68569314 -0.03926846 1.2736826 0.51690364]
[-0.03926846 0.18800406 -0.32171276 -0.11798123]
[ 1.2736826 -0.32171276 3.1131783 1.2963878 ]
[ 0.51690364 -0.11798123 1.2963878 0.58241445]]
Numpy
[[ 0.68569351 -0.03926846 1.27368233 0.5169038 ]
[-0.03926846 0.18800403 -0.32171275 -0.11798121]
[ 1.27368233 -0.32171275 3.11317942 1.29638747]
[ 0.5169038 -0.11798121 1.29638747 0.58241432]]
同じ結果になるのを確認できました。本来の誤差はこれぐらいですね。
TensorFlowで相関行列
データを平均と標準偏差で標準化して、グラム行列の期待値を求めると相関行列になります。同様に計算してみましょう。
from sklearn.datasets import load_iris
import keras.backend as K
import tensorflow as tf
import numpy as np
def tf_corrcoef(input_tensor):
mean, var = tf.nn.moments(input_tensor, axes=0, keep_dims=True)
stddev = tf.sqrt(var)
normalize = (input_tensor - mean) / (stddev+K.epsilon())
n_sample = tf.cast(tf.shape(input_tensor)[0], tf.float32)
gram_matrix = tf.matmul(normalize, normalize, transpose_a=True)
return gram_matrix / n_sample
if __name__ == "__main__":
iris_X, iris_y = load_iris(return_X_y=True)
iris_X_tensor = K.variable(iris_X)
corr_tensor = tf_corrcoef(iris_X_tensor)
print("TensorFlow")
print(K.eval(corr_tensor))
print()
print("Numpy")
print(np.corrcoef(iris_X, rowvar=False))
TensorFlow
[[ 1.0000006 -0.10936929 0.87175435 0.8179536 ]
[-0.10936929 0.9999995 -0.42051592 -0.35654384]
[ 0.87175435 -0.42051592 1.0000011 0.9627567 ]
[ 0.8179536 -0.35654384 0.9627567 0.9999992 ]]
Numpy
[[ 1. -0.10936925 0.87175416 0.81795363]
[-0.10936925 1. -0.4205161 -0.35654409]
[ 0.87175416 -0.4205161 1. 0.9627571 ]
[ 0.81795363 -0.35654409 0.9627571 1. ]]
ほぼ同じになりました。TensorFlowのコードを見ると、分散共分散行列と相関行列が似ているというのがよくわかります。
TensorFlowでの分散共分散行列、相関行列の導出(テンソル版)
さて同じことをテンソルでやってみましょう。少し楽しくなってきますよ。
Irisデータセットでは3種類のあやめのデータがあり、あやめの品種ごとに50個ずつのデータがあるため、(150, 4)の行列を(3, 50, 4)のテンソルに変形し、カテゴリー間の分散共分散行列・相関行列を求めることができます。さてこれはforループを使わずにどうやるでしょうか(ちなみにNumpyのコードはただの検証用なので手抜きでforループ使います)。TensorFlowの本領発揮です。
from sklearn.datasets import load_iris
import keras.backend as K
import tensorflow as tf
import numpy as np
def tf_cov_tensor(input_tensor):
# 行列版のmeanのaxisと、shapeのindexを変えただけ
mean = tf.reduce_mean(input_tensor, axis=1, keepdims=True)
mean_adjust = input_tensor - mean
n_sample = tf.cast(tf.shape(input_tensor)[1] - 1, tf.float32) #不偏分散(N-1)で計算
gram_matrix = tf.matmul(mean_adjust, mean_adjust, transpose_a=True)
return gram_matrix / n_sample
def tf_corrcoef_tensor(input_tensor):
# 行列版のmeanのaxisと、shapeのindexを変えただけ
mean, var = tf.nn.moments(input_tensor, axes=1, keep_dims=True)
stddev = tf.sqrt(var)
normalize = (input_tensor - mean) / (stddev+K.epsilon())
n_sample = tf.cast(tf.shape(input_tensor)[1], tf.float32)
gram_matrix = tf.matmul(normalize, normalize, transpose_a=True)
return gram_matrix / n_sample
if __name__ == "__main__":
iris_X, iris_y = load_iris(return_X_y=True)
iris_X = iris_X.reshape(3, 50, 4) # 順に50個ずつ並んでいるため
iris_X_tensor = K.variable(iris_X)
cov_tensor = tf_cov_tensor(iris_X_tensor)
print("TensorFlow 分散共分散行列")
print(K.eval(cov_tensor))
print()
print("Numpy 分散共分散行列")
for i in range(3):
print(np.cov(iris_X[i], rowvar=False))
print()
print("--------------------------")
corr_tensor = tf_corrcoef_tensor(iris_X_tensor)
print("TensorFlow 相関行列")
print(K.eval(corr_tensor))
print()
print("Numpy 相関行列")
for i in range(3):
print(np.corrcoef(iris_X[i], rowvar=False))
print()
実は分散共分散行列、相関行列とも平均や分散、サンプル数を求める際の軸を変えただけです。それ以外は一切変えていません。このグラム行列のアプローチがテンソルの階数に対してとても頑強であるのがわかるでしょう。
TensorFlow 分散共分散行列
[[[0.12424893 0.10029797 0.01613878 0.01054693]
[0.10029797 0.14517957 0.01168164 0.01143674]
[0.01613878 0.01168164 0.03010613 0.00569796]
[0.01054693 0.01143674 0.00569796 0.01149388]]
[[0.26643267 0.08518368 0.18289796 0.05577959]
[0.08518368 0.09846939 0.08265302 0.04120408]
[0.18289796 0.08265302 0.22081633 0.07310203]
[0.05577959 0.04120408 0.07310203 0.03910612]]
[[0.40434283 0.09376322 0.30328983 0.04909386]
[0.09376322 0.10400411 0.07137959 0.04762857]
[0.30328983 0.07137959 0.30458766 0.04882448]
[0.04909386 0.04762857 0.04882448 0.07543267]]]
Numpy 分散共分散行列
[[0.12424898 0.10029796 0.01613878 0.01054694]
[0.10029796 0.14517959 0.01168163 0.01143673]
[0.01613878 0.01168163 0.03010612 0.00569796]
[0.01054694 0.01143673 0.00569796 0.01149388]]
[[0.26643265 0.08518367 0.18289796 0.05577959]
[0.08518367 0.09846939 0.08265306 0.04120408]
[0.18289796 0.08265306 0.22081633 0.07310204]
[0.05577959 0.04120408 0.07310204 0.03910612]]
[[0.40434286 0.09376327 0.3032898 0.04909388]
[0.09376327 0.10400408 0.07137959 0.04762857]
[0.3032898 0.07137959 0.30458776 0.04882449]
[0.04909388 0.04762857 0.04882449 0.07543265]]
--------------------------
TensorFlow 相関行列
[[[0.99999976 0.74678016 0.26387393 0.27909127]
[0.74678016 0.9999998 0.17669453 0.2799726 ]
[0.26387393 0.17669453 0.9999985 0.30630782]
[0.27909127 0.2799726 0.30630782 0.9999985 ]]
[[0.99999976 0.5259102 0.7540485 0.54646057]
[0.5259102 0.9999992 0.5605217 0.663998 ]
[0.7540485 0.5605217 0.9999997 0.7866677 ]
[0.54646057 0.663998 0.7866677 0.9999988 ]]
[[0.99999934 0.45722756 0.86422443 0.2811075 ]
[0.45722756 0.99999946 0.40104443 0.5377276 ]
[0.86422443 0.40104443 0.99999976 0.322108 ]
[0.2811075 0.5377276 0.322108 0.9999988 ]]]
Numpy 相関行列
[[1. 0.74678037 0.26387409 0.27909157]
[0.74678037 1. 0.17669463 0.27997289]
[0.26387409 0.17669463 1. 0.30630821]
[0.27909157 0.27997289 0.30630821 1. ]]
[[1. 0.52591072 0.75404896 0.54646107]
[0.52591072 1. 0.56052209 0.66399872]
[0.75404896 0.56052209 1. 0.78666809]
[0.54646107 0.66399872 0.78666809 1. ]]
[[1. 0.45722782 0.86422473 0.28110771]
[0.45722782 1. 0.40104458 0.53772803]
[0.86422473 0.40104458 1. 0.32210822]
[0.28110771 0.53772803 0.32210822 1. ]]
結果はこの通りです。forループを使ったNumpyと、テンソルによる一括計算のTensorFlowとで一緒の結果が出ています。
Numpyで主成分分析
せっかくなのでおまけで主成分分析もやってみましょう。まずはNumpyから固めていきます。
import numpy as np
from sklearn.datasets import load_iris
from sklearn.decomposition import PCA
def numpy_pca(data):
mean = np.mean(iris_X, axis=0, keepdims=True)
data_mean_adj = data - mean
cov = np.cov(data_mean_adj, rowvar=False)
U, S, V = np.linalg.svd(cov)
print("次元削減の固有ベクトル")
U_reduce = U[:, :2]
print(U_reduce)
# 次元削減
project = np.dot(data_mean_adj, U_reduce)
# 次元の復元
data_rec = np.dot(project, U_reduce.T)+mean
print("次元削減→復元")
print(data_rec[:5, :])
def sklearn_pca(data):
pca = PCA(n_components=2)
pca.fit(data)
print("次元削減の固有ベクトル")
print(pca.components_.T)
# 次元削減
project = pca.transform(data)
# 次元の復元
data_rec = pca.inverse_transform(project)
print("次元削減→復元")
print(data_rec[:5, :])
if __name__ == "__main__":
iris_X, iris_y = load_iris(return_X_y=True)
print("Numpy")
numpy_pca(iris_X)
print()
print("Scikit-learn")
sklearn_pca(iris_X)
上がNumpyでの実装で、下がScikit-learnの実装です。上下が等しくなるか確かめます。
Numpy
次元削減の固有ベクトル
[[-0.36158968 -0.65653988]
[ 0.08226889 -0.72971237]
[-0.85657211 0.1757674 ]
[-0.35884393 0.07470647]]
次元削減→復元
[[5.08718247 3.51315614 1.4020428 0.21105556]
[4.75015528 3.15366444 1.46254138 0.23693223]
[4.70823155 3.19151946 1.30746874 0.17193308]
[4.64598447 3.05291508 1.46083069 0.23636736]
[5.07593707 3.5221472 1.36273698 0.19458132]]
Scikit-learn
次元削減の固有ベクトル
[[ 0.36158968 0.65653988]
[-0.08226889 0.72971237]
[ 0.85657211 -0.1757674 ]
[ 0.35884393 -0.07470647]]
次元削減→復元
[[5.08718247 3.51315614 1.4020428 0.21105556]
[4.75015528 3.15366444 1.46254138 0.23693223]
[4.70823155 3.19151946 1.30746874 0.17193308]
[4.64598447 3.05291508 1.46083069 0.23636736]
[5.07593707 3.5221472 1.36273698 0.19458132]]
同じ結果が出てきてました実装できました。固有ベクトルの符号は反転していても結果には影響ありません。必要なら固有値の大きい順にソートする必要がありますが、たいていSVDで計算すると固有値が大きい順に返ってきているので抜いてしまいました。必要なら入れてください。
軽く説明すると、主成分分析とは分散共分散行列の固有値、固有ベクトルを求めて次元の削減・復元を行うものです。分散共分散行列を特異値分解していますが、分散共分散行列は対称行列なので、特異値と固有値が一致する性質があります。したがって特異値分解で固有ベクトルが求められるというわけですね。次元の復元・削減は内積で定義されます。復元する際は転置させるのをお忘れずに。
次はTensorFlowで行ってみましょう。
TensorFlowで主成分分析(行列編)
これまでの総まとめです。行ってみましょう。
from sklearn.datasets import load_iris
import tensorflow as tf
import keras.backend as K
import numpy as np
def tf_pca(data_tensor):
mean = tf.reduce_mean(data_tensor, axis=0, keepdims=True)
mean_adj = data_tensor - mean
n_sample = tf.cast(tf.shape(data_tensor)[0]-1, tf.float32)
cov = tf.matmul(mean_adj, mean_adj, transpose_a=True) / n_sample
S, U, V = tf.linalg.svd(cov)
# 次元削減
U_reduce = U[:, :2]
project = tf.matmul(mean_adj, U_reduce)
# 次元の復元
data_rec = tf.matmul(project, U_reduce, transpose_b=True) + mean
return U_reduce, data_rec[:5,:]
if __name__ == "__main__":
iris_X, iris_y = load_iris(return_X_y=True)
iris_X_tensor = K.variable(iris_X)
U_reduce, data_rec = tf_pca(iris_X_tensor)
print("次元削減")
print(K.eval(U_reduce))
print("次元の復元")
print(K.eval(data_rec))
次元削減
[[ 0.3615897 0.6565389 ]
[-0.0822689 0.72971344]
[ 0.85657203 -0.17576654]
[ 0.35884395 -0.07470739]]
次元の復元
[[5.087183 3.513156 1.4020433 0.21105546]
[4.750156 3.1536634 1.4625413 0.23693264]
[4.7082324 3.1915188 1.3074684 0.17193341]
[4.6459856 3.0529141 1.4608302 0.23636782]
[5.0759377 3.5221472 1.3627372 0.19458115]]
TensorFlowでも主成分分析を実装することができました! 1つだけ注意が必要なのが、NumpyでのSVDがU,S,Vの順で返ってくるのに対して、TensorFlowのSVDはS,U,Vの順で返ってきます。そこだけご注意ください。
TensorFlowで主成分分析(テンソル編)
今度はこれの発展で、テンソルの主成分分析をしてみましょう。分散共分散行列のときと同様に、Irisデータをカテゴリー別にreshapeして3階テンソルの主成分分析をします。難しそうですが、実は行列のときとほぼ同じで簡単ですよ。
def tf_pca_tensor(data_tensor):
mean = tf.reduce_mean(data_tensor, axis=1, keepdims=True)
mean_adj = data_tensor - mean
n_sample = tf.cast(tf.shape(data_tensor)[1]-1, tf.float32)
cov = tf.matmul(mean_adj, mean_adj, transpose_a=True) / n_sample
S, U, V = tf.linalg.svd(cov)
# 次元削減
U_reduce = U[:, :, :2]
project = tf.matmul(mean_adj, U_reduce)
# 次元の復元
data_rec = tf.matmul(project, U_reduce, transpose_b=True) + mean
return U_reduce, data_rec
if __name__ == "__main__":
iris_X, iris_y = load_iris(return_X_y=True)
iris_X_category = iris_X.reshape(3,50,4)
iris_X_tensor = K.variable(iris_X_category)
U_reduce, data_rec = tf_pca_tensor(iris_X_tensor)
U_reduce_numpy = K.eval(U_reduce)
data_rec_numpy = K.eval(data_rec)
print("次元削減")
print(U_reduce_numpy)
print("次元の復元")
print(data_rec_numpy[:,:5,:])
IrisデータセットはSetosa、Versicolor、Virginicaからなるので、次元削減のほうは上からSetosaの固有ベクトル、Versicolorの固有ベクトル、Virginicaの固有ベクトルです。次元の復元のほうは同様にカテゴリー別の復元されたデータです。
次元削減
[[[ 0.6662065 0.60592383]
[ 0.7363595 -0.619614 ]
[ 0.09478703 0.491636 ]
[ 0.07042406 0.08502112]]
[[ 0.68672365 -0.66908926]
[ 0.30534697 0.5674646 ]
[ 0.62366307 0.3433276 ]
[ 0.21498369 0.3353052 ]]
[[ 0.7410169 -0.1652592 ]
[ 0.2032877 0.7486431 ]
[ 0.62789184 -0.16942744]
[ 0.12377448 0.61928815]]]
次元の復元
[[[5.0642343 3.5198314 1.4605051 0.2495466 ]
[4.8444753 3.0337324 1.5057105 0.23027138]
[4.6692014 3.2194185 1.3614676 0.20557266]
[4.6488 3.0683255 1.3989843 0.20550658]
[4.99465 3.600933 1.4009184 0.239621 ]]
[[6.922698 2.956136 4.8783827 1.475807 ]
[6.323751 3.0066733 4.682796 1.4878612 ]
[6.8798127 3.034254 4.9462857 1.5235907 ]
[5.5654635 2.5421278 3.8540974 1.1702498 ]
[6.503533 2.8620985 4.5992317 1.402742 ]]
[[6.64672 3.3944762 5.5867853 2.365265 ]
[5.904784 2.7259467 4.975331 1.8624883 ]
[7.0546994 3.0398786 5.949754 2.0533147 ]
[6.446078 2.8112872 5.436328 1.9014462 ]
[6.658459 3.0725257 5.608772 2.1022937 ]]]
実際のIrisデータの値があるのでこちらと見比べてください。カテゴリー別だと1~5、51~55、101~105までと比較すればいいです。次元削減したので多少誤差はあるもののほぼ復元できていますね。
TensorFlowのmatmul強いですね。次にカテゴリー別に違う固有ベクトルを使って、次元削減の可視化をしてみましょう。
from sklearn.datasets import load_iris
import tensorflow as tf
import keras.backend as K
import numpy as np
def tf_pca_tensor_project(data_tensor):
mean = tf.reduce_mean(data_tensor, axis=1, keepdims=True)
mean_adj = data_tensor - mean
n_sample = tf.cast(tf.shape(data_tensor)[1], tf.float32)
cov = tf.matmul(mean_adj, mean_adj, transpose_a=True)
S, U, V = tf.linalg.svd(cov)
# 次元削減
U_reduce = U[:, :, :2]
project = tf.matmul(mean_adj, U_reduce)
# 次元の復元
data_rec = tf.matmul(project, U_reduce, transpose_b=True) + mean
return project, data_rec
import matplotlib.pyplot as plt
if __name__ == "__main__":
iris_X, iris_y = load_iris(return_X_y=True)
iris_X_category = iris_X.reshape(3,50,4)
iris_X_tensor = K.variable(iris_X_category)
project, data_rec = tf_pca_tensor_project(iris_X_tensor)
project_numpy = K.eval(project)
data_rec_numpy = K.eval(data_rec)
print(project_numpy.shape) # (3, 50, 2)
print(data_rec_numpy.shape) # (3, 50, 4)
cm = plt.get_cmap("Set1")
categories = ["Setosa", "Versicolor", "Virginica"]
for i in range(3):
ax = plt.subplot(2,2,i+1)
ax.plot(project_numpy[i,:,0], project_numpy[i,:,1], ".", color=cm(i))
ax.set_title(categories[i])
ax = plt.subplot(2,2,4)
ax.plot(project_numpy[:,:,0].reshape(-1, 1), project_numpy[:,:,1].reshape(-1,1), ".", color=cm(3))
ax.set_title("All")
plt.show()
先程の関数の返り値を、固有ベクトルから次元削減後の値に変えただけです。
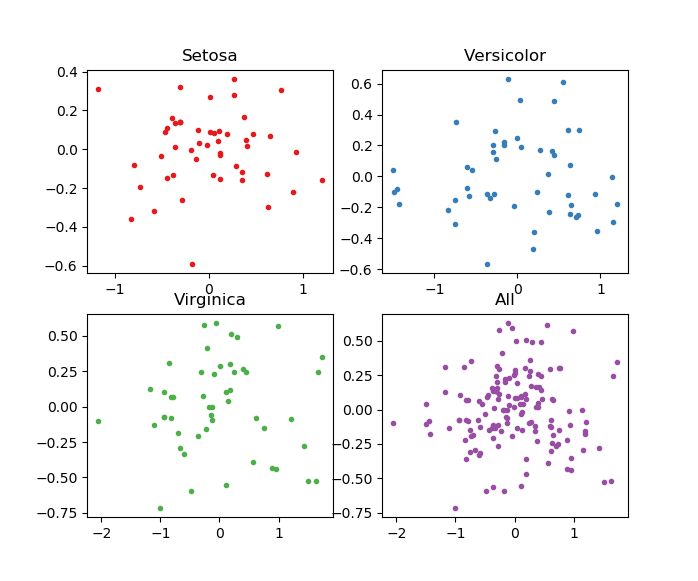
ポイントはカテゴリー別に異なる固有ベクトルを使っている点です。したがって、Allで示されるプロットは、全体を一括でやった場合と異なるものとなっています。
まとめ
これまでのグラム行列のTensorFlowでの求め方からはじまり、グラム行列、分散共分散行列、相関行列の関係を見てきました。それらの総まとめとして、TensorFlowでの分散共分散行列、相関行列の計算や、TensorFlowでカテゴリー別の主成分分析をするというところまで行けました。こうしてみるとテンソルって強力なんですね。
Shikoan's ML Blogの中の人が運営しているサークル「じゅ~しぃ~すくりぷと」の本のご案内
技術書コーナー
北海道の駅巡りコーナー

