多変量分布のKLダイバージェンスの実装

分布間の差を定量化する手法として、KLダイバージェンスが機械学習では広く使われますが、多変量への拡張の実装面の話が必要になったので検証してみました。KDTreeを使った推定がノンパラへの拡張も期待できそうで便利でした。
目次
きっかけ
多変量分布のKLダイバージェンスを計算したいが、理論的な解説はあっても実装的な部分が気になったので確かめてみたという話。「Multi variable kl divergence python」で検索していたら、KDTreeを使って推定ベースで計算していたものがありました。
https://gist.github.com/atabakd/ed0f7581f8510c8587bc2f41a094b518
なぜ多変量分布で考える必要があるのか
普通のKLダイバージェンスは、scipy.stats.entropyで簡単に求められます。
参考:https://www.haya-programming.com/entry/2018/01/22/151849
しかし、これはサンプル間の演算で、例えば以下のように「分布は同じだが、サンプルの順番が入れ替わったケース」では同一分布(ダイバージェンスが0)と判定してくれません。
from scipy.stats import entropy
import numpy as np
x = np.array([[0.1, 0.2], [0.3, -0.4]])
y = np.array([[0.3, -0.4], [0.1, 0.2]])
# サンプルの順番も分布も等しい場合
print(entropy(x, x, base=2))
# [ 0. inf]
# サンプルの順番は異なるが、分布は等しい場合
print(entropy(x, y, base=2))
# [0.79248125 inf]
xとyの違いは、1番目のサンプルと2番目のサンプルを入れ替えただけですが、「x, x」でエントロピーを計算した場合と、「x, y」でエントロピーを計算したときで結果が異なります。両者は分布が同じなので一緒であってほしいです。
この理由は単純で、多変量分布のKLダイバージェンスで考えていないからです。
多変量正規分布のKLダイバージェンス
多変量正規分布の場合のKLダイバージェンスの結果は理論的に示せます(正規分布というパラメトリックな過程をおいた場合です)。優秀な記事が大量にあるので詳細は割愛しますが、
$$\mathrm{KL}[P\,||\,Q] = \frac{1}{2} \left[ (\mu_2 – \mu_1)^T \Sigma_2^{-1} (\mu_2 – \mu_1) + \mathrm{tr}(\Sigma_2^{-1} \Sigma_1) – \ln \frac{|\Sigma_1|}{|\Sigma_2|} – n \right]$$
https://statproofbook.github.io/P/mvn-kl.html
となります。ここで、$\mu, \Sigma$は平均のベクトルと、分散共分散行列を示します。$A^T$は転置行列、$A^{-1}$は逆行列、$\mathrm{tr}(A)$は行列のトレース、$|A|$は行列式を表します。また、$n$は次元数です。
一見これで終わりに見えますが、これを解析的に使おうとするといろいろ問題があります。
- 計算量が重いオペレーションが多い(逆行列、行列式)。サンプルや次元が増えたときに遅そう
- 統計的な厳密性を求めるなら、サンプルが正規分布に従わない場合は、この公式を使うのはおかしい
多変量分布のKLダイバージェンスの推定値
プログラム的に求めたい場合は、解析的な解よりも、推定値で十分なことが多いです。ググってたらこちらのコードを見つけました。
https://gist.github.com/atabakd/ed0f7581f8510c8587bc2f41a094b518
# https://mail.python.org/pipermail/scipy-user/2011-May/029521.html
import numpy as np
def KLdivergence(x, y):
"""Compute the Kullback-Leibler divergence between two multivariate samples.
Parameters
----------
x : 2D array (n,d)
Samples from distribution P, which typically represents the true
distribution.
y : 2D array (m,d)
Samples from distribution Q, which typically represents the approximate
distribution.
Returns
-------
out : float
The estimated Kullback-Leibler divergence D(P||Q).
References
----------
Pérez-Cruz, F. Kullback-Leibler divergence estimation of
continuous distributions IEEE International Symposium on Information
Theory, 2008.
"""
from scipy.spatial import cKDTree as KDTree
# Check the dimensions are consistent
x = np.atleast_2d(x)
y = np.atleast_2d(y)
n,d = x.shape
m,dy = y.shape
assert(d == dy)
# Build a KD tree representation of the samples and find the nearest neighbour
# of each point in x.
xtree = KDTree(x)
ytree = KDTree(y)
# Get the first two nearest neighbours for x, since the closest one is the
# sample itself.
r = xtree.query(x, k=2, eps=.01, p=2)[0][:,1]
s = ytree.query(x, k=1, eps=.01, p=2)[0]
# There is a mistake in the paper. In Eq. 14, the right side misses a negative sign
# on the first term of the right hand side.
return -np.log(r/s).sum() * d / n + np.log(m / (n - 1.))
元の論文のタイトルは「連続分布のKLダイバージェンスの推定」みたいなタイトルなのでほぼピンポイントの内容です。KDTreeを使って実装しているのがポイントで、(おそらく)ノンパラメトリックな設定でもいけるはずです。
実際に試してみる
先程の順番を入れ替えた例で試してみます。
x = np.array([[0.1, 0.2], [0.3, -0.4]])
y = np.array([[0.3, -0.4], [0.1, 0.2]])
print(KLdivergence(x, x))
# -inf
print(KLdivergence(x, y))
# -inf
Gistのコメント欄にもありますが、推定値であって解析解ではないので、ダイバージェンスなのにマイナスがついていたり割りと精度面でガバい部分が多いですが、Infを0に置き換えたり、絶対値を取ればなんとかなりそうな気はします。
なにより速そうなのがいいですね。
これ以外のやり方だと、例えば列単位でソートしてscipy.stats.entropyを取るなどがありますが、実践的な例で試したら異なる分布なのにInfが出てかなり悩ましい結果になったので、この手法のほうが便利なこともあるかもしれません。
多変量正規分布での検証
平均をシフト
def mean_shift_test():
mean_shift = np.linspace(-2.0, 2.0, num=11)
dim = 10
n = 100
klds = []
for shift in mean_shift:
a = np.random.multivariate_normal(np.zeros(dim), np.identity(dim), n)
b = np.random.multivariate_normal(np.zeros(dim)+shift, np.identity(dim), n)
klds.append(KLdivergence(a, b))
klds = np.array(klds)
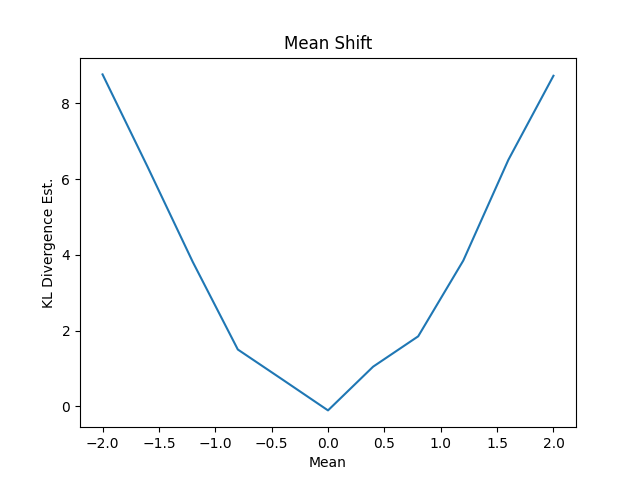
このように機械的にシフトしていくケースではわかりやすい結果になりました。
平均ベクトルにノイズを足していってその強度を制御する場合はどうでしょうか?
def mean_noisy_shift_test():
mean_shift = np.linspace(-2.0, 2.0, num=11)
dim = 10
n = 100
klds = []
np.random.seed(1234)
noise = np.random.randn(dim)
for shift in mean_shift:
a = np.random.multivariate_normal(np.zeros(dim), np.identity(dim), n)
b = np.random.multivariate_normal(np.zeros(dim)+noise*shift, np.identity(dim), n)
klds.append(KLdivergence(a, b))
klds = np.array(klds)
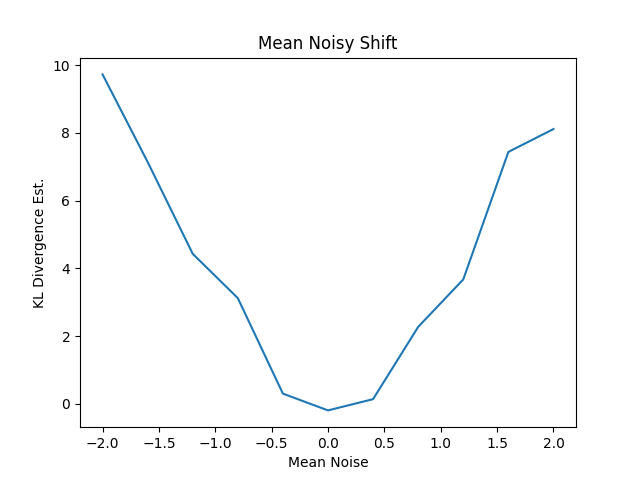
これもわかりやすい結果になっています。ただ、一部でKLDの値にマイナスが出ています。あくまで推定値なので。
[ 9.72472931 7.13935711 4.42720607 3.11991228 0.3001449 -0.19482345
0.13746173 2.27096145 3.6715492 7.43575229 8.11107166]
共分散をシフト
今度は(分散)共分散をシフトさせます。分散共分散行列には独特の特徴があるのでシミュレーションする上では注意します。
- 対角成分は分散を示す。それ以外は共分散を示す
- 対称行列であり、上三角行列の転置が下三角行列になる
- i番目の系列とj番目の系列の共分散は一緒なため
def std_shift_test():
cov_shift = np.linspace(-2.0, 2.0, num=11)
dim = 10
n = 100
klds = []
np.random.seed(1234)
noise = np.random.randn(dim, dim)
for shift in cov_shift:
# make covariance matrix
shift_cov = np.identity(dim)
upper_indices = np.triu_indices(dim, k=1)
shift_cov[upper_indices] = noise[upper_indices] * shift
lower_indices = np.tril_indices(dim, k=-1)
shift_cov[lower_indices] = noise.T[lower_indices] * shift
# print(shift_cov)
a = np.random.multivariate_normal(np.zeros(dim), np.identity(dim), n)
b = np.random.multivariate_normal(np.zeros(dim), shift_cov, n)
klds.append(KLdivergence(a, b))
このようにシフトさせていくと次のようになりました。うまくいっているようです。
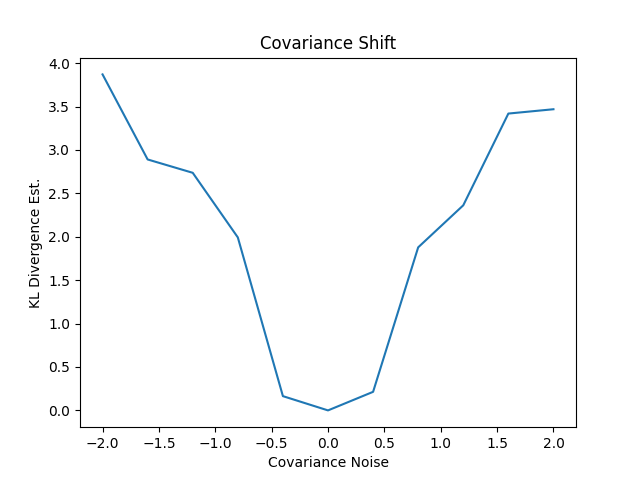
この共分散行列の作り方見慣れないので、dim=3, シフトの数を5に落として表示してみます(私もこんなやり方初めてやりました)。
-- -2.0
[[ 1. 2.38195139 -2.86541394]
[ 2.38195139 1. -1.77432588]
[-2.86541394 -1.77432588 1. ]]
-- -1.0
[[ 1. 1.19097569 -1.43270697]
[ 1.19097569 1. -0.88716294]
[-1.43270697 -0.88716294 1. ]]
-- 0.0
[[ 1. -0. 0.]
[-0. 1. 0.]
[ 0. 0. 1.]]
-- 1.0
[[ 1. -1.19097569 1.43270697]
[-1.19097569 1. 0.88716294]
[ 1.43270697 0.88716294 1. ]]
-- 2.0
[[ 1. -2.38195139 2.86541394]
[-2.38195139 1. 1.77432588]
[ 2.86541394 1.77432588 1. ]]
確かに分散共分散行列の性質を満たしています。
サンプル数を変える
分布同士の比較になるので、Aのサンプル数とBのサンプル数を変えて比較することも可能になります。以下のようなケースです
- Aの従う分布と、Bの従う分布を異なる分布として考える(本来これらの分布は未知だが、天下り的に既知として考える)
- Aからは10固定で、Bからはサンプル数を変えてサンプリングする
- Bのサンプリング数は(10, 50, 100, 500, 1000)と変動
- サンプリング数が少ないほうがKLDの変動は大きいはずなので、乱数を変えて5回試行
コードに直すと次のようになります。
def sample_size_test():
sample_size = [10, 50, 100, 500, 1000]
np.random.seed(1234)
dim = 3
n = 100
a = np.random.multivariate_normal(np.zeros(dim), np.identity(dim), n)
# mean
shift_mean = np.random.randn(dim) * 0.1
# covariance
noise = np.random.randn(dim, dim)
shift_cov = np.identity(dim)
upper_indices = np.triu_indices(dim, k=1)
shift_cov[upper_indices] = noise[upper_indices]
lower_indices = np.tril_indices(dim, k=-1)
shift_cov[lower_indices] = noise.T[lower_indices]
klds = []
for i in range(5):
item = []
for sample in sample_size:
b = np.random.multivariate_normal(shift_mean, shift_cov, sample)
item.append(KLdivergence(a, b))
klds.append(item)
平均のベクトルも共分散のベクトルもわずかに変えています。グラフにプロットすると次の通り
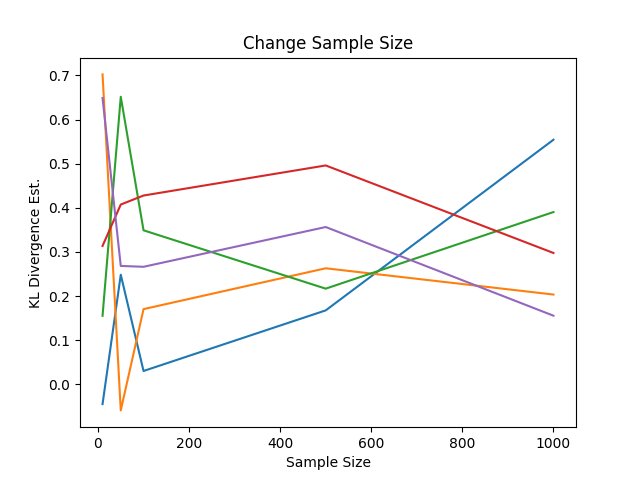
予想どおり、サンプル数が少ないほど試行回数間の変動は大きく、サンプル数を増やすと変動は小さくなりました。解析的にはこの2つの分布のKLDは何らの定数になりますが、あくまで推定値のアルゴリズムなので、1000まで増やしても変動があります。
応用例としては、極端にデータ数が多いケースでKLDを求めたいときに、ブートストラップ法が使えそうということでしょうね。例えばデータ数が1億ぐらいあって、その中から1000~1万ぐらいランダムサンプリングしてKLDを計算しても、1億で計算したときとほとんど変わらないはずです。
また、求めたKLDの値がサンプル数に依存しないというのも嬉しい点です(KLDの定義から明らかかもしれませんが)。
正規分布以外でも使う
この方法のメリットとして、データの分布に依存した計算がでてこないので、おそらくノンパラメトリックなアプローチでも使えると思います(理論的な部分は自信ない)。元の論文のアブストラクトを読むと
Abstract—We present a method for estimating the KL divergence between continuous densities and we prove it converges almost surely. Divergence estimation is typically solved estimating the densities first. Our main result shows this intermediate step is unnecessary and that the divergence can be either estimated using the empirical cdf or k-nearest-neighbour density estimation, which does not converge to the true measure for finite k. The convergence proof is based on describing the statistics of our estimator using waiting-times distributions, as the exponential or Erlang. We illustrate the proposed estimators and show how they compare to existing methods based on density estimation, and we also outline how our divergence estimators can be used for solving the two-sample problem
要旨-連続密度間のKLダイバージェンスを推定する方法を提示し、ほぼ確実に収束することを証明する。ダイバージェンスの推定は、一般的に、まず密度を推定することで解決される。本論文では、この中間ステップが不要であり、ダイバージェンスは経験的cdfまたはk-nearest-neighbour密度推定を用いて推定することができるが、これは有限のkに対して真の尺度に収束しないことを示す。収束証明は、指数またはアーランなどの待ち時間分布を用いた推定器の統計量を記述することに基づく。提案する推定器を図示し、密度推定に基づく既存の方法との比較を示す。また、我々のダイバージェンス推定器が2標本問題の解決にどのように利用できるかを概説する。
ここでポイントなのは、連続な確率密度関数であればいいのであって、どこにもこれが正規分布限定であるとは書いていないのです。なので、分布が正規分布ではない場合もいけるのではないかと思って調べてみます。一様分布でいってみます。
- 基準となる分布は-1~1の一様分布とする
- 比較対象の分布は-1-s~1+sの一様分布として、sの値を0~5と変動させる
def change_distribution_test():
mean_shift = np.linspace(0, 5, num=10)
dim = 10
n = 100
klds = []
for shift in mean_shift:
a = np.random.uniform(low=-1, high=1, size=(n, dim))
b = np.random.uniform(low=-1-shift, high=1+shift, size=(n, dim))
klds.append(KLdivergence(a, b))
klds = np.array(klds)
plt.plot(mean_shift, klds)
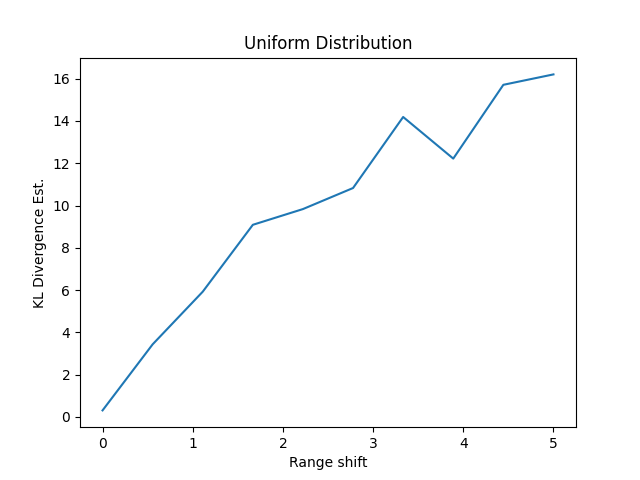
Range Shiftの値が大きくなるほど分布が離れていくので、KLDは右肩上がりになるはずです。実際にその通りなので、ほぼ期待通りの結果になりました。
実際に多変量のKLダイバージェンスとして解析的に出ている公式は、ほぼ多変量正規分布限定なので、これが多変量の任意分布でいけそうというのはおもしろそうな点です。
まとめ
- KDTreeを使ったKLダイバージェンスの推定は割りと使えそう
- 平均をシフトしても、共分散をシフトしても、あるいは2つのデータのサンプル数が異なる場合も計算できた
- 多変量の任意分布でもいけそうでノンパラメトリックなアプローチとして使えるかもしれない
- あくまで推定値なので、値がマイナスになることがある。そこを気にする場合は注意
Shikoan's ML Blogの中の人が運営しているサークル「じゅ~しぃ~すくりぷと」の本のご案内
技術書コーナー
北海道の駅巡りコーナー

